题目内容
已知两函数f(x)=7x2-28x-c,g(x)=2x3+4x2-40x.
(1)对任意x∈[-3,3],都有f(x)≤g(x)成立,求实数c的取值范围;
(2)存在x∈[-3,3],使f(x)≤g(x)成立,求实数c的取值范围;
(3)对任意x1,x2∈[-3,3],都有f(x1)≤g(x2),求实数c的取值范围.
(1)对任意x∈[-3,3],都有f(x)≤g(x)成立,求实数c的取值范围;
(2)存在x∈[-3,3],使f(x)≤g(x)成立,求实数c的取值范围;
(3)对任意x1,x2∈[-3,3],都有f(x1)≤g(x2),求实数c的取值范围.
考点:二次函数的性质
专题:函数的性质及应用,导数的概念及应用
分析:构造函数k(x)=f(x)-g(x)=-2x3+3x2+12x-c,x∈[-3,3],
(1)求出k(x)的最大值k(x)大≤0即可.
(2)求出k(x)的最大值k(x)小≤0即可.
(3)运用算求出f(x)大≤g(x)小即可.
(1)求出k(x)的最大值k(x)大≤0即可.
(2)求出k(x)的最大值k(x)小≤0即可.
(3)运用算求出f(x)大≤g(x)小即可.
解答:
解:∵f(x)=7x2-28x-c,g(x)=2x3+4x2-40x.
k(x)=f(x)-g(x)=-2x3+3x2+12x-c,x∈[-3,3],
k′(x)=-6x2+6x+12,
-6x2+6x+12=0,x=-1,x=2,
-6x2+6x+12>0,-1<x<2
-6x2+6x+12<0,x<-1或x>2,
k(-3)=-63-c,k(3)=117-c,
k(-1)=-7-c,k(2)=20-c,
最大值为117-c,最小值-63-c,
(1)∵对任意x∈[-3,3],都有f(x)≤g(x)成立,
∴117-c≤0,即c≥117,
(2)∵存在x∈[-3,3],使f(x)≤g(x)成立,
∴-63-c≤0,
即c≥-63,
(3)f(x)=7x2-28x-c,g(x)=2x3+4x2-40x.
f(x)大=f(-3)=147-c,g′(x)=6x2+8x-40,
与用导数可求解得出g(x)小=g(2)=-80,
∵对任意x1,x2∈[-3,3],都有f(x1)≤g(x2),
∴147-c≤-80,
c≥227,
k(x)=f(x)-g(x)=-2x3+3x2+12x-c,x∈[-3,3],
k′(x)=-6x2+6x+12,
-6x2+6x+12=0,x=-1,x=2,
-6x2+6x+12>0,-1<x<2
-6x2+6x+12<0,x<-1或x>2,
| x | [-3,-1) | -1 | (-1,2) | 2 | (2,3] |
| y′ | - | 0 | + | 0 | - |
| y | 减 | 极小值 | 增 | 极大值 | 减 |
k(-1)=-7-c,k(2)=20-c,
最大值为117-c,最小值-63-c,
(1)∵对任意x∈[-3,3],都有f(x)≤g(x)成立,
∴117-c≤0,即c≥117,
(2)∵存在x∈[-3,3],使f(x)≤g(x)成立,
∴-63-c≤0,
即c≥-63,
(3)f(x)=7x2-28x-c,g(x)=2x3+4x2-40x.
f(x)大=f(-3)=147-c,g′(x)=6x2+8x-40,
与用导数可求解得出g(x)小=g(2)=-80,
∵对任意x1,x2∈[-3,3],都有f(x1)≤g(x2),
∴147-c≤-80,
c≥227,
点评:本题综合考查了不等式的恒成立问题,转化为最大值,最小值的比较,关键是能分清任意与存在的区别与联系,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若命题p:2是偶数,命题q:2是3的约数,则下列结论中正确的是( )
| A、“p∨q”为假 |
| B、“p∨q”为真 |
| C、“p∧q”为真 |
| D、以上都不对 |
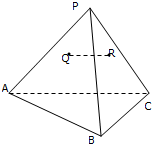 如图,已知P为△ABC所在平面内一点,Q、R是△PAB、△PBC的重心,求证:直线QR∥平面ABC.
如图,已知P为△ABC所在平面内一点,Q、R是△PAB、△PBC的重心,求证:直线QR∥平面ABC.