题目内容
在平面直角坐标系xOy中，已知椭圆C：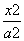
＋
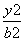＝1(a>b>0)过点P(2,1)，且离心率e＝
.
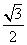(1)求椭圆C的方程；
(2)直线l的斜率为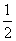
，直线l与椭圆C交于A，B两点．求△PAB的面积的最大值．
解：(1)∵e＝
＝，
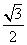∴e2＝
＝
＝
，∴a2＝4b2.
又椭圆C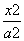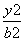：＋＝1(a>b>0)过点P(2,1)，
∴
＋
＝1.∴a2＝8，b2＝2.
故所求椭圆方程为
＋
＝1.
(2)设l的方程为y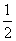＝x＋m，点A(x1，y1)，B(x2，y2)，
联立
整理，得x2＋2mx＋2m2－4＝0.
Δ＝4m2－8m2＋16>0，
解得|m|<2.
x1＋x2＝－2m，x1·x2＝2m2－4.
当且仅当m2＝2即m＝±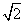
时取得最大值．
∴△PAB面积的最大值为2.
练习册系列答案
相关题目
，当
时，实数
的取值范围是（ ）
A．
B.
C.
D.
。
的函数
，
且对任意
，
，试写出具有上述性质的一个函数 
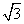，则p＝( )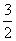
B.
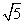
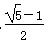D.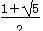
－
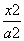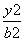＝1(a>0，b>0)的左、右焦点，P为双曲线上一点，若∠F1PF2＝90°，且△F1PF2的三边长成等差数列，则双曲线的离心率是( )
的图象在点(－1,2)处的切线与坐标轴围成的三角形的面积等于( )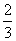
B.
C.
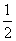D.
的图像关于直线
对称，且图像上
和
的值； (Ⅱ)若
，求
的值．