题目内容
已知函数f（x）=2+
，则
f（x）dx= ．
| 2x-x2 |
| ∫ | 2 0 |
考点：定积分的简单应用
专题：计算题,导数的概念及应用
分析：
f（x）dx的几何意义是以（1，2）为圆心，1为半径的圆的面积，可得结论．
| ∫ | 2 0 |
解答：
解：∵y=2+
，
∴（x-1）2+（y-2）2=1（y≥2），
∴
f（x）dx的几何意义是以（1，2）为圆心，1为半径的圆的面积的一半加正方形面积，即
π+4．
故答案为：
π+4．
| 2x-x2 |
∴（x-1）2+（y-2）2=1（y≥2），
∴
| ∫ | 2 0 |
| 1 |
| 2 |
故答案为：
| 1 |
| 2 |
点评：本题考查定积分求面积，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
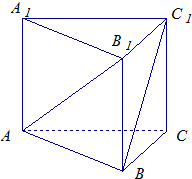在正三棱柱ABC-A1B1C1中，AB1⊥BC1，求BC1与平面ABB1A1所成角的正弦值．（正三棱柱：上下底面为正三角形的直棱柱，底面边长不一定等于侧棱长）已知等差数列{an}的前n项和为Sn（n∈N*），且an=2n+λ，若数列{Sn}在n≥7时为递增数列，则实数λ的取值范围为（ ）
| A、（-15，+∞） |
| B、[-15，+∞） |
| C、[-16，+∞） |
| D、（-16，+∞） |