题目内容
已知函数f(x)=|x-1|,g(x)=-|x+3|+a,a∈R
(1)解关于x的不等式g(x)>6;
(2)若函数y=2f(x)的图象恒在函数y=g(x)的上方,求实数a的取值范围.
(1)解关于x的不等式g(x)>6;
(2)若函数y=2f(x)的图象恒在函数y=g(x)的上方,求实数a的取值范围.
考点:绝对值不等式的解法,函数恒成立问题
专题:不等式的解法及应用
分析:(1)不等式即-|x+3|+a>6,即|x+3|<a-6,分当a≤6时和当a>6时两种情况,分别求得不等式的解集.,
(2)由题意可得2f(x)-g(x)>0,即a<2|x-1|+|x+3|.设h(x)=2|x-1|+|x+3|=
,利用单调性求的h(x)的最小值,可得a的范围.
(2)由题意可得2f(x)-g(x)>0,即a<2|x-1|+|x+3|.设h(x)=2|x-1|+|x+3|=
|
解答:
解:(1)不等式即-|x+3|+a>6,即|x+3|<a-6,
当a≤6时无解;
当a>6时,由-(a-6)<x+3<a-6,即3-a<x<a-9,
求得不等式解集为(3-a,a-9)(a>6).
(2)y=2f(x)图象恒在g(x)图象上方,故2f(x)-g(x)>0,等价于a<2|x-1|+|x+3|.
设h(x)=2|x-1|+|x+3|=
,根据函数h(x)的单调减区间为(-∞,1]、增区间为(1,+∞),
可得当x=1时,h(x)取得最小值为4,∴a<4时,函数y=2f(x)的图象恒在函数y=g(x)的上方.
当a≤6时无解;
当a>6时,由-(a-6)<x+3<a-6,即3-a<x<a-9,
求得不等式解集为(3-a,a-9)(a>6).
(2)y=2f(x)图象恒在g(x)图象上方,故2f(x)-g(x)>0,等价于a<2|x-1|+|x+3|.
设h(x)=2|x-1|+|x+3|=
|
可得当x=1时,h(x)取得最小值为4,∴a<4时,函数y=2f(x)的图象恒在函数y=g(x)的上方.
点评:本题主要考查绝对值不等式的解法,函数的恒成立问题,利用单调性求函数的最值,体现了转化、分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目
在△ABC中,其中有两解的是( )
| A、a=8,b=15,A=30° |
| B、a=30,b=25,A=150° |
| C、a=72,b=50,A=135° |
| D、a=18,b=16,A=60° |
一个几何体的三视图如图所示,则该几何体的体积为( )


| A、48-16π |
| B、96-4π |
| C、96-8π |
| D、48-4π |
方程ln(x+1)-
=0,(x>0)的根存在的大致区间是( )
| 2 |
| x |
| A、(0,1) |
| B、(1,2) |
| C、(2,e) |
| D、(3,4) |
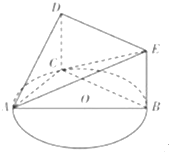 如图,已知三角形ABC内接于圆O,AB为圆O的直径,四边形DCBE为平行四边形,CD⊥平面ABC,AB=2,tan∠EAB=
如图,已知三角形ABC内接于圆O,AB为圆O的直径,四边形DCBE为平行四边形,CD⊥平面ABC,AB=2,tan∠EAB=