题目内容
设集合A={x|y=log2(x-2)},B={x|x2-3x-4<0},则A∪B= .
考点:并集及其运算
专题:集合
分析:求出A中函数的定义域确定出A,求出B中不等式的解集确定出B,求出A与B的并集即可.
解答:
解:由函数y=log2(x-2),得到x-2>0,即x>2,
∴A=(2,+∞),
由B中的不等式变形得:(x-4)(x+1)<0,
解得:-1<x<4,即B=(-1,4),
则A∪B=(-1,+∞).
故答案为:(-1,+∞)
∴A=(2,+∞),
由B中的不等式变形得:(x-4)(x+1)<0,
解得:-1<x<4,即B=(-1,4),
则A∪B=(-1,+∞).
故答案为:(-1,+∞)
点评:此题考查了并集及其运算,熟练掌握并集的定义是解本题的关键.

练习册系列答案
相关题目
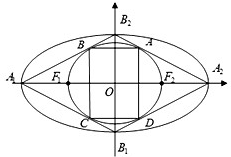 如图,椭圆
如图,椭圆| x2 |
| a2 |
| y2 |
| b2 |
| S1 |
| S2 |
A、
| ||||
B、2
| ||||
C、
| ||||
D、
|
已知向量
=(3,1),
=(x,-2),
=(0,2),若
⊥(
-
),则实数x的值为( )
| a |
| b |
| c |
| a |
| b |
| c |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
若(
)x-1>9,则x的取值范围是( )
| 1 |
| 3 |
| A、(-1,+∞) |
| B、(-∞,2) |
| C、(-∞,-1) |
| D、[2,+∞) |