题目内容
已知抛物线
 过点
过点 。
。
(Ⅰ)求抛物线 的方程及其准线方程;
的方程及其准线方程;
(Ⅱ) 过抛物线焦点 的直线
的直线 与抛物线
与抛物线 相交于两点
相交于两点
 ,点
,点 在抛物线
在抛物线 的准线上,且满足直线
的准线上,且满足直线 平行
平行 轴,试判断坐标原点
轴,试判断坐标原点 与直线
与直线 的关系,并证明你的结论。
的关系,并证明你的结论。
(Ⅰ)  ,
,
(Ⅱ) 坐标原点 在直线
在直线 上.
上.
【解析】
试题分析:在求抛物线的方程式,注意将抛物线上的一个点的坐标带入抛物线的方程即可求得,对于第二问,注意答题的习惯,应该先写出点和直线的关系,再证明点在直线上,证明的时候就应用了三点共线的条件,应用的直线的斜率相等做的.
试题解析:(1) 将M(1,-2)代入y2=2px, 得(-2)2=2p·1,所以p=2.
故所求的抛物线C的方程为: 3分
3分
其准线方程为x=-1. 4分
(2)判断坐标原点 在直线
在直线 上, 5分
上, 5分
现证明如下:依题意可设过F的直线l方程为:x=my+1(m ),
),
设 ,
,
由 得:
得:
依题意可知 ,且
,且 9分
9分
又∵
又∵ , ∴
, ∴
即证坐标原点 在直线
在直线 上 12分
上 12分
(说明:直线l方程也可设为:y=k(x-1),但需加入对斜率不存在情况的讨论,否则扣1分)
考点:抛物线的方程,抛物线的准线,点与直线的位置关系,证明三点共线的方法.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 的最小正周期为( )
的最小正周期为( ) B.
B. C.
C. D.
D.
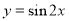 是( )
是( )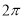 的偶函数
的偶函数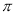 的偶函数
的偶函数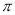 的奇函数
的奇函数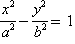 (a>0,b>0),若过右焦点F且倾斜角为30°的直线与双曲线的右支有
(a>0,b>0),若过右焦点F且倾斜角为30°的直线与双曲线的右支有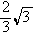 ) C.[2,+∞) D.[
) C.[2,+∞) D.[ 的单调减区间是( )
的单调减区间是( ) B.
B. C.
C. D.
D.
 是以
是以 为直角顶点的等腰直角三角形,其中
为直角顶点的等腰直角三角形,其中 ,
, (
( ),则
),则
 中,
中, 是棱
是棱 的中点,则
的中点,则 与
与 所成角的余弦值为( )
所成角的余弦值为( )
 B.
B. C.
C.  D.
D.
 ,
, ,则△ABC的面积等于 .
,则△ABC的面积等于 . 中,角
中,角 所对的边分别是
所对的边分别是 ,若
,若 ,则
,则