题目内容
1．已知两条直线l1：x+2my+6=0，l2：（m-2）x+3my+2m=0问：当m为何值时，l1与l2
（1）平行；
（2）垂直．
分析 （1）由2m（m-2）-3m=0，解得m，经过验证即可得出．
（2）对m分类讨论，利用两条直线相互垂直的充要条件即可得出．
解答 解：（1）由2m（m-2）-3m=0，解得m=0或$\frac{7}{2}$．
经过验证m=0或$\frac{7}{2}$都满足条件．
（2）m=0时，两条直线不垂直，舍去．
m≠0时，由$-\frac{1}{2m}$×$（-\frac{m-2}{3m}）$=-1，解得m=$\frac{1}{2}$或$-\frac{2}{3}$．
∴m=$\frac{1}{2}$或$-\frac{2}{3}$，两条直线相互垂直．
点评 本题考查了两条直线相互平行与垂直的充要条件，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
9．下列说法正确的是（ ）
| A． | 函数$y=sin（2x+\frac{π}{3}）$在区间$（-\frac{π}{3}，\frac{π}{6}）$内单调递增 | |
| B． | 函数y=cos4x的最小正周期为2π | |
| C． | 函数y=cos（x+$\frac{π}{3}$）的图象是关于点（$\frac{π}{6}$，0）成中心对称的图形 | |
| D． | 函数y=tan（x+$\frac{π}{3}$）的图象是关于直线x=$\frac{π}{6}$成轴对称的图形 |
13．把函数$y=sin（x+\frac{π}{4}）$的图象向左平移$\frac{π}{4}$个单位长度，再将横坐标压缩到原来的$\frac{1}{2}$，所得函数的解析式为（ ）
| A． | y=sin2x | B． | $y=sin（2x+\frac{π}{8}）$ | C． | y=cos2x | D． | $y=cos\frac{1}{2}x$ |
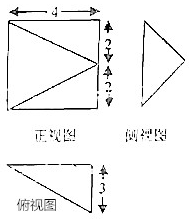一个几何体的三视图如图所示，则该几何体的表面积是32+4$\sqrt{13}$．