题目内容
若f(cosx)=cos2x,则f(sin75°)= .
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:已知等式右边利用二倍角的余弦函数公式化简,确定出f(x)解析式,将x=sin75°代入计算即可求出值.
解答:
解:∵f(cosx)=cos2x=2cos2x-1,
∴f(x)=2x2-1,
∵sin75°=sin(45°+30°)=
,
∴f(sin75°)=2sin275°-1=2×
-1=1+
-1=
.
故答案为:
∴f(x)=2x2-1,
∵sin75°=sin(45°+30°)=
| ||||
| 4 |
∴f(sin75°)=2sin275°-1=2×
8+4
| ||
| 16 |
| ||
| 2 |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
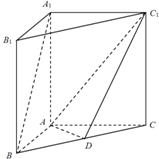 直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=1,AA1=
直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=1,AA1=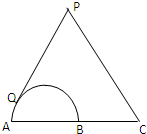 如图,点C为半圆的直径AB延长线上一点,AB=BC=2,过动点P作半圆的切线PQ,若
如图,点C为半圆的直径AB延长线上一点,AB=BC=2,过动点P作半圆的切线PQ,若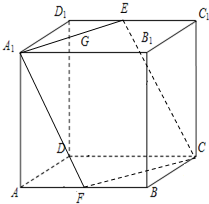 如图,在正方体ABCD-A1B1C1D1中,E、F分别为C1D1与AB的中点,则A1B1与截面A1ECF所成角的大小为
如图,在正方体ABCD-A1B1C1D1中,E、F分别为C1D1与AB的中点,则A1B1与截面A1ECF所成角的大小为