题目内容
 已知椭圆
已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 2 |
(Ⅰ)求该椭圆的方程;
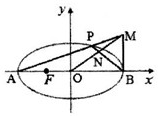
(Ⅱ)如图,直线BM⊥AB,BM交AP于M,OM交BP于N,求点N到点Q(0,2)的距离的最大值.
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(I)利用|PF|≥a-c,S△PFA=
(a-c)•|yP|≤
(a-c)•b,a2=b2+c2,联立解得即可.
(II)设M(2,m),则直线AM的方程为:y=
(x+2).代入椭圆的方程可得关于x的一元二次方程及根与系数的关系,进而得到直线BP、直线OM的方程.联立可得点N的轨迹方程,再利用点到圆上的点的距离求法即可得出.
| 1 |
| 2 |
| 1 |
| 2 |
(II)设M(2,m),则直线AM的方程为:y=
| m |
| 4 |
解答:
解:(I)|PF|=a+ex≥a-c=2-
,S△PFA=
(a-c)•|yP|≤
(a-c)•b=
-1,
联立
,解得a=2,b=c=
.
∴该椭圆的方程为
+
=1;
(II)设M(2,m),则直线AM的方程为:y=
(x+2).
代入椭圆的方程可得(m2+8)x2+4m2x+4m2-32=0,
∴-2+xP=-
,化为xP+2=
.
∴kBP=
=
=-
.
由直线BP:y=-
(x-2),
直线OM的方程为:y=
x.
联立
,化为y2=-x(x-2)(x≠0).
即(x-1)2+y2=1(x≠0),圆心C(1,0),半径r=1.
∴|QN|min=|CN|+1=
+1=
+1.
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
联立
|
| 2 |
∴该椭圆的方程为
| x2 |
| 4 |
| y2 |
| 2 |
(II)设M(2,m),则直线AM的方程为:y=
| m |
| 4 |
代入椭圆的方程可得(m2+8)x2+4m2x+4m2-32=0,
∴-2+xP=-
| 4m2 |
| m2+8 |
| 32 |
| m2+8 |
∴kBP=
| yP |
| xP-2 |
| m(xP+2) |
| 4(xP-2) |
| 2 |
| m |
由直线BP:y=-
| 2 |
| m |
直线OM的方程为:y=
| m |
| 2 |
联立
|
即(x-1)2+y2=1(x≠0),圆心C(1,0),半径r=1.
∴|QN|min=|CN|+1=
| 12+22 |
| 5 |
点评:本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得关于x的一元二次方程及根与系数的关系、直线的方程、两点间的距离公式、点到圆上的点的最值距离的求法等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 在如图所示的空间几何体中,平面ACD⊥平面ABC,△ACD与△ACB是边长为2的等边三角形,BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.
在如图所示的空间几何体中,平面ACD⊥平面ABC,△ACD与△ACB是边长为2的等边三角形,BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.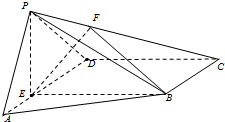 如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD,AD∥BC,AD⊥CD,BC=ED=2AE,F为PC上一点,且CF=2FP.
如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD,AD∥BC,AD⊥CD,BC=ED=2AE,F为PC上一点,且CF=2FP.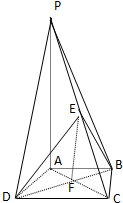 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=2,AD=4,DC=3,PA=5,E∈PC,AC∩BD=F.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=2,AD=4,DC=3,PA=5,E∈PC,AC∩BD=F.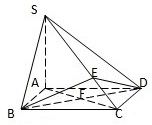 已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,E是SC上的任意一点.
已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,E是SC上的任意一点.