题目内容
2.化简求值:(1)$\root{3}{{a}^{\frac{9}{2}\sqrt{{a}^{-3}}}}$÷$\sqrt{\root{3}{{a}^{-7}•}\root{3}{{a}^{13}}}$
(2)lg52+$\frac{2}{3}lg8+lg5lg20+{(lg2)^2}$
(3)${0.001^{-\frac{1}{3}}}-{(\frac{7}{8})^0}+{16^{\frac{3}{4}}}+{(\sqrt{2}•\root{3}{3})^6}$.
分析 根据指数幂和对数的运算性质即可求出.
解答 解:(1)原式=$({a}^{\frac{9}{2}}•{a}^{-\frac{3}{2}})^{\frac{1}{3}}$÷$({a}^{-\frac{7}{3}}•{a}^{\frac{13}{3}})^{\frac{1}{2}}$=${a}^{3×\frac{1}{2}}$÷${a}^{2×\frac{1}{2}}$=a÷a=1
(2)原式=2lg5+2lg2+lg5(1+lg2)+(lg2)2=2(lg2+lg5)+lg5+lg2(lg5+lg2)=2+lg5+lg2=3,
(3)原式=$0.{1}^{3×(-\frac{1}{3})}$-1+${2}^{4×\frac{3}{4}}$+${2}^{\frac{1}{2}×6}$•${3}^{\frac{1}{3}×6}$=10-1+8+72=89.
点评 本题考查了指数幂和对数的运算性质,属于基础题.

练习册系列答案
相关题目
17.设全集是实数集R,A={x|x2>4},$B=\left\{{x|\frac{2}{x-1}≥1}\right\}$,则(∁RA)∩B=( )
| A. | [-2,3] | B. | [-2,3) | C. | (1,2] | D. | [1,2) |
11.由幂函数y=$\sqrt{x}$和幂函数y=x3图象围成的封闭图形的面积为( )
| A. | $\frac{1}{12}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{5}{12}$ |
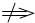 ”.填空:
”.填空: