题目内容
数列{an}中,a1=1,前n项和为Sn=
an,n∈N*,则通项公式an= .
| n+2 |
| 3 |
考点:数列的函数特性
专题:等差数列与等比数列
分析:由已知条件利用递推思想求出数列的前4项,总结规律,猜想数列的通项公式.
解答:
解:∵数列{an}中,a1=1,前n项和为Sn=
an,n∈N*,
∴S2=1+a2=
a2,解得a2=3=1+2,
S3=4+a3=
a3,解得a3=6=1+2+3,
S4=10+a4=
a4,解得a4=10=1+2+3+4.
由此猜想:an=1+2+3+4+…+n=
.
故答案为:
.
| n+2 |
| 3 |
∴S2=1+a2=
| 4 |
| 3 |
S3=4+a3=
| 5 |
| 3 |
S4=10+a4=
| 6 |
| 3 |
由此猜想:an=1+2+3+4+…+n=
| n(n+1) |
| 2 |
故答案为:
| n(n+1) |
| 2 |
点评:本题考查数列的通项公式的求法,是基础题,解题时要认真审题,注意猜想法的合理运用.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
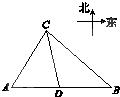 如图,港口A北偏东30°方向的C处有一检查站,港口正东方向的B处有一轮船,距离检查站7海里,该轮船从B处沿正西方向航行3海里后到达D处观测站,已知观测站与检查站距离5海里,则此时轮船离港口A有
如图,港口A北偏东30°方向的C处有一检查站,港口正东方向的B处有一轮船,距离检查站7海里,该轮船从B处沿正西方向航行3海里后到达D处观测站,已知观测站与检查站距离5海里,则此时轮船离港口A有