题目内容
14.已知函数$g(x)=\left\{\begin{array}{l}sin\frac{π}{2}x,\;\;x<0\\{log_4}(x+1),x>0\end{array}\right.$,则函数y=g(x)-x的零点个数是3.分析 在同一坐标系中画出函数$g(x)=\left\{\begin{array}{l}sin\frac{π}{2}x,\;\;x<0\\{log_4}(x+1),x>0\end{array}\right.$的图象和y=x的图象,分析两图象交点的个数,可得答案.
解答 解:函数$g(x)=\left\{\begin{array}{l}sin\frac{π}{2}x,\;\;x<0\\{log_4}(x+1),x>0\end{array}\right.$的图象如下图所示:
由图可得,函数y=g(x)与函数函数y=x的图象有三个交点,
故函数y=g(x)-x的零点个数是3个,
故答案为:3
点评 本题考查的知识点是函数的零点及个数判断,将函数的零点转化为函数图象的交点,是解答的关键.

练习册系列答案
相关题目
11.已知集合$A=\{x|y=\sqrt{4-{x^2}}\}$,B={y|y=x2-x+1,0<x<2},则A∩B=( )
| A. | $(\frac{3}{4},2]$ | B. | [2,3) | C. | (1,2] | D. | (-∞,-2]∪[2,+∞) |
19.已知圆锥的母线长为5,底面周长为6π,则它的体积为( )
| A. | 10π | B. | 12π | C. | 15π | D. | 36π |
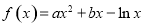 (
(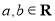 ).
). 时,求函数
时,求函数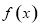 在
在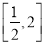 上的最大值和最小值;
上的最大值和最小值;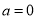 时,是否存在正实数
时,是否存在正实数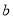 ,当
,当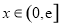 (
(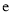 是自然对数底数)时,函数
是自然对数底数)时,函数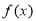 的最小值是3,若存在,求出
的最小值是3,若存在,求出