题目内容
4.已知数列{an}的前n项和为Sn,且Sn=$\frac{4}{3}$(an-1),则满足不等式an>2n+16的最小正整数n的值为( )| A. | 12 | B. | 14 | C. | 16 | D. | 17 |
分析 利用递推关系、等比数列的通项公式可得an,再利用指数函数的单调性即可得出.
解答 解:∵Sn=$\frac{4}{3}$(an-1),∴当n=1时,${a}_{1}=\frac{4}{3}({a}_{1}-1)$,解得a1=4.
当n≥2时,Sn-1=$\frac{4}{3}({a}_{n-1}-1)$,可得an=$\frac{4}{3}({a}_{n}-{a}_{n-1})$,化为:an=4an-1.
∴数列{an}是等比数列,首项为4,公比为4.
∴an=4n.
不等式an>2n+16化为:22n>2n+16,∴2n>n+16,解得n>16.
∴满足不等式an>2n+16的最小正整数n的值为17.
故选:D.
点评 本题考查了递推关系、等比数列的通项公式、指数函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
11.在等差数列中,S17=34,则a2+a16等于( )
| A. | 17 | B. | 6 | C. | 4 | D. | 2 |
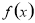 在R上是奇函数,且满足
在R上是奇函数,且满足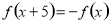 ,当
,当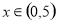 时,
时,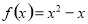 ,则
,则 ( )
( ) 为曲边的曲边形(如下图阴影部分)面积为 .
为曲边的曲边形(如下图阴影部分)面积为 .
 ,则
,则 =( )
=( ) B.
B. C.
C. D.
D.
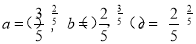 ,则a, b,c的大小关系是( )
,则a, b,c的大小关系是( )