题目内容
6.已知数列{an}满足a1=1,(n+1)an+1=nan(n∈N*).(1)求{an}的通项公式.
(2)若bn=$\frac{2}{n+1}$an,数列{bn}的前n项和为Tn,求证:Tn<2.
分析 (1)由a1=1,(n+1)an+1=nan(n∈N*),可得$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{n}{n+1}$.当n≥2时,an=${a}_{1}•\frac{{a}_{2}}{{a}_{1}}•\frac{{a}_{3}}{{a}_{2}}$•…•$\frac{{a}_{n}}{{a}_{n-1}}$,即可得出;
(2)bn=$\frac{2}{n+1}$an=$\frac{2}{n(n+1)}$=2$(\frac{1}{n}-\frac{1}{n+1})$.利用“裂项求和”即可证明.
解答 (1)解:∵a1=1,(n+1)an+1=nan(n∈N*),
∴$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{n}{n+1}$.
∴当n≥2时,an=${a}_{1}•\frac{{a}_{2}}{{a}_{1}}•\frac{{a}_{3}}{{a}_{2}}$•…•$\frac{{a}_{n}}{{a}_{n-1}}$=$1×\frac{1}{2}×\frac{2}{3}$×…×$\frac{n-1}{n}$=$\frac{1}{n}$,当n=1时也成立,
∴an=$\frac{1}{n}$.
(2)证明:bn=$\frac{2}{n+1}$an=$\frac{2}{n(n+1)}$=2$(\frac{1}{n}-\frac{1}{n+1})$.
∴数列{bn}的前n项和为Tn=2$[(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{n}-\frac{1}{n+1})]$=2$(1-\frac{1}{n})$<2.
∴Tn<2.
点评 本题考查了数列的通项公式、“裂项求和”、“累乘求积”、不等式的性质,考查了推理能力与计算能力,属于中档题.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案| A. | $\lim_{n→∞}{a_n}$和$\lim_{n→∞}{S_n}$都存在 | B. | $\lim_{n→∞}{a_n}$和$\lim_{n→∞}{S_n}$都不存在 | ||
| C. | $\lim_{n→∞}{a_n}$存在,$\lim_{n→∞}{S_n}$不存在 | D. | $\lim_{n→∞}{a_n}$不存在,$\lim_{n→∞}{S_n}$存在 |
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{9}{4}$ |
 ,则
,则 =( )
=( ) B.
B. C.
C. D.
D.
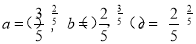 ,则a, b,c的大小关系是( )
,则a, b,c的大小关系是( )