题目内容
6.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点分别为F1(-c,0),F2(c,0),以线段F1F2为直径的圆与双曲线在第二象限的交点为P,若直线PF2与圆E:(x-$\frac{c}{2}$)2+y2=$\frac{{b}^{2}}{16}$相切,则双曲线的渐近线方程是( )| A. | y=±x | B. | y=±2x | C. | y=±$\sqrt{3}$x | D. | y=±$\sqrt{2}$x |
分析 求出|PF1|=4r=b,所以|PF2|=2a+b,因此b2+(2a+b)2=4c2,即可求出双曲线的渐近线方程.
解答 解:设切点为M,则EM∥PF1,又$\frac{{F}_{2}E}{{F}_{2}{F}_{1}}$=$\frac{1}{4}$,所以|PF1|=4r=b,所以|PF2|=2a+b,因此b2+(2a+b)2=4c2,
所以b=2a,所以渐近线方程为y=±2x.
故选:B.
点评 本题考查双曲线的方程与性质,考查直线与圆的位置关系,属于中档题.

练习册系列答案
相关题目
16.中国传统文化中不少优美的古诗词很讲究对仗,如“明月松间照,清泉石上流”中明月对清泉同为自然景物,明和清都是形容词,月和泉又都是名词,数学除了具有简洁美、和谐美、奇异美外,也具有和古诗词中对仗类似的对称美.请你判断下面四个选项中,体现数学对称美的是( )
| A. | “$1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{100}$”表示成“$\sum_{k=1}^{100}{\frac{1}{k}}$” | |
| B. | 平面上所有二次曲线的一般形式均可表示成:Ax2+Bxy+Cy2+Dx+Ey+F=0 | |
| C. | 正弦定理:$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$ | |
| D. | 123456789×9+10=1111111111 |
1.运行如图所示框图的相应程序,若输入a,b的值分别为log43和log34,则输出M的值是( )

| A. | 0 | B. | 1 | C. | 3 | D. | -1 |
11.已知函数$f(x)=\left\{\begin{array}{l}{log_{\frac{1}{3}}}x,x>0\\{2^x},x≤0\end{array}\right.$,若$f(a)>\frac{1}{2}$,则实数a的取值范围是( )
| A. | $({0,\frac{{\sqrt{3}}}{3}})$ | B. | (-1,0] | C. | $({-1,\frac{{\sqrt{3}}}{3}})$ | D. | $({-1,0})∪({0,\frac{{\sqrt{3}}}{3}})$ |
18.已知x,y满足约束条件$\left\{\begin{array}{l}x-y-2≤0\\ 5x-3y-12≥0\\ y≤3\end{array}\right.$当目标函数z=ax+by(a>0,b>0)在该约束条件下取得最小值1时,则$\frac{1}{3a}+\frac{2}{b}$的最小值为( )
| A. | $4+2\sqrt{2}$ | B. | $4\sqrt{2}$ | C. | $3+2\sqrt{2}$ | D. | $3+\sqrt{2}$ |
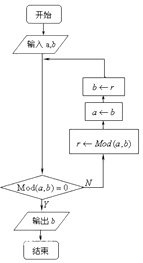 辗转相除法,又名欧几里得算法,乃求两个正整数之最大公因子的算法.它是已知最古老的算法,在中国则可以追溯至东汉出现的《九章算术》,图中的程序框图所表述的算法就是欧几里得辗转相除法,若输入a=5280,b=12155,则输出的b=55.
辗转相除法,又名欧几里得算法,乃求两个正整数之最大公因子的算法.它是已知最古老的算法,在中国则可以追溯至东汉出现的《九章算术》,图中的程序框图所表述的算法就是欧几里得辗转相除法,若输入a=5280,b=12155,则输出的b=55.