题目内容
18.已知x,y满足约束条件$\left\{\begin{array}{l}x-y-2≤0\\ 5x-3y-12≥0\\ y≤3\end{array}\right.$当目标函数z=ax+by(a>0,b>0)在该约束条件下取得最小值1时,则$\frac{1}{3a}+\frac{2}{b}$的最小值为( )| A. | $4+2\sqrt{2}$ | B. | $4\sqrt{2}$ | C. | $3+2\sqrt{2}$ | D. | $3+\sqrt{2}$ |
分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,代入目标函数可得3a+b=1,再运用“1”的代换利用基本不等式求得$\frac{1}{3a}+\frac{2}{b}$的最小值.
解答 解:由约束条件$\left\{\begin{array}{l}x-y-2≤0\\ 5x-3y-12≥0\\ y≤3\end{array}\right.$作出可行域如图,
联立$\left\{\begin{array}{l}{x-y-2=0}\\{5x-3y-12=0}\end{array}\right.$,解得A(3,1),
化目标函数z=ax+by为$y=-\frac{a}{b}x+\frac{z}{b}$,
由图可知,当直线$y=-\frac{a}{b}x+\frac{z}{b}$过A时,直线在y轴上的截距最小,z有最小值为3a+b=1,
则$\frac{1}{3a}+\frac{2}{b}$=($\frac{1}{3a}+\frac{2}{b}$)(3a+b)=3+$\frac{b}{3a}+\frac{6a}{b}$$≥3+2\sqrt{2}$.
当且仅当a=$\frac{\sqrt{2}-1}{3}$,b=2-$\sqrt{2}$时取“=”.
故选:C.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法及数学转化思想方法,是中档题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
8.按照图如图所示的程序框图执行,若输出结果为s=31,则M处条件是( )


| A. | k<32? | B. | k>32? | C. | k<16? | D. | k>16? |
6.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点分别为F1(-c,0),F2(c,0),以线段F1F2为直径的圆与双曲线在第二象限的交点为P,若直线PF2与圆E:(x-$\frac{c}{2}$)2+y2=$\frac{{b}^{2}}{16}$相切,则双曲线的渐近线方程是( )
| A. | y=±x | B. | y=±2x | C. | y=±$\sqrt{3}$x | D. | y=±$\sqrt{2}$x |
10.在平面直角坐标系xoy中,直线l:y=2x-4,圆C的半径为1,圆心在直线l上,若圆C上存在点M,且M在圆D:x2+(y+1)2=4上,则圆心C的横坐标a的取值范围是( )
| A. | $[{\frac{3}{5},2}]$ | B. | $[{0,\frac{12}{5}}]$ | C. | $[{2-\frac{2}{5}\sqrt{5},2+\frac{2}{5}\sqrt{5}}]$ | D. | $[{0,2-\frac{2}{5}\sqrt{5}}]∪[{2+\frac{2}{5}\sqrt{5},4}]$ |
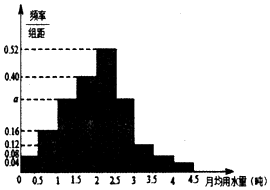 水是地球上宝贵的资源,由于价格比较便宜在很多不缺水的城市居民经常无节制的使用水资源造成严重的资源浪费.某市政府为了提倡低碳环保的生活理念鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),[1,1.5),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.
水是地球上宝贵的资源,由于价格比较便宜在很多不缺水的城市居民经常无节制的使用水资源造成严重的资源浪费.某市政府为了提倡低碳环保的生活理念鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),[1,1.5),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.