题目内容
14.已知抛物线E:y2=2px(p>0)的焦点为F,过F且垂直于x轴的直线与抛物线E交于A,B两点,E的准线与x轴交于点C,△CAB的面积为4,以点D(3,0)为圆心的圆D过点A,B.(Ⅰ)求抛物线E和圆D的方程;
(Ⅱ)若斜率为k(|k|≥1)的直线m与圆D相切,且与抛物线E交于M,N两点,求$\overrightarrow{FM}•\overrightarrow{FN}$的取值范围.
分析 (Ⅰ)利用,△CAB的面积为4,以点D(3,0)为圆心的圆D过点A,B,即可求抛物线E和圆D的方程;
(Ⅱ)设直线m:y=kx+b(|k|≥1),则$\frac{|3k+b|}{\sqrt{{k}^{2}+1}}$=2$\sqrt{2}$,即k2+6kb+b2=8,联立y=kx+b与抛物线,利用韦达定理及向量数量积公式,即可得出结论.
解答 解:(Ⅰ)由题意,$F(\frac{p}{2},0),A(\frac{p}{2},p),B(\frac{p}{2},-p),C(-\frac{p}{2},0),{S_{△ABC}}={p^2}$,(1分)
由p2=4得p=2,圆D半径R=2$\sqrt{2}$,(3分)
所以抛物线E:y2=4x,圆(x-3)2+y2=8.(4分)
(Ⅱ)设直线m:y=kx+b(|k|≥1),
则$\frac{|3k+b|}{\sqrt{{k}^{2}+1}}$=2$\sqrt{2}$,即k2+6kb+b2=8,①
联立y=kx+b与抛物线得ky2-4y+4b=0,△=16-16kb,(5分)
由①知kb≤1,即△≥0(6分)
所以方程ky2-4y+4b=0有两个实数根y1,y2,且y1+y2=$\frac{4}{k}$,y1y2=$\frac{4b}{k}$(7分)
$\overrightarrow{FM}•\overrightarrow{FN}$=$\frac{1}{16}$[(y1y2)2-4(y1+y2)2+24y1y2+16]=$\frac{{b}^{2}+6kb{+}^{2}-4}{{k}^{2}}$=$\frac{4}{{k}^{2}}$(11分)
因为|k|≥1,所以$\overrightarrow{FM}•\overrightarrow{FN}$的取值范围是(0,4].(12分)
点评 本题考查抛物线与圆的方程,考查直线与抛物线的位置关系,考查韦达定理、向量知识的运用,属于中档题.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案| A. | [1,3] | B. | (1,3] | C. | [2,3] | D. | (2,3] |
| A. | [kπ-$\frac{11π}{24}$,kπ+$\frac{π}{24}$](k∈Z) | B. | $[kπ+\frac{3π}{8},kπ+\frac{7π}{8}](k∈Z)$ | ||
| C. | $[2kπ-\frac{π}{4},2kπ+\frac{3π}{4}](k∈Z)$ | D. | $[2kπ+\frac{3π}{4},2kπ+\frac{7π}{4}](k∈Z)$ |
| A. | [-3,3] | B. | [-1,2] | C. | [-3,2] | D. | (-1,2] |
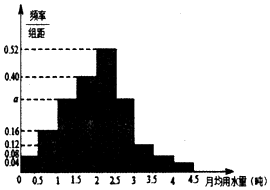 水是地球上宝贵的资源,由于价格比较便宜在很多不缺水的城市居民经常无节制的使用水资源造成严重的资源浪费.某市政府为了提倡低碳环保的生活理念鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),[1,1.5),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.
水是地球上宝贵的资源,由于价格比较便宜在很多不缺水的城市居民经常无节制的使用水资源造成严重的资源浪费.某市政府为了提倡低碳环保的生活理念鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),[1,1.5),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.