题目内容
18.现抛掷两枚骰子,记事件A为“朝上的2个数之和为偶数”,事件B为“朝上的2个数均为偶数”,则P(B|A)=( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{2}$ |
分析 用列举法求出事件A、事件AB所包含的基本事件的个数,根据条件概率公式P(B|A)=$\frac{{n}_{AB}}{{n}_{A}}$,即可得到结论.
解答 解:事件A为“朝上的2个数之和为偶数“所包含的基本事件有:(1,1),(2,2),(3,3),(4,4),(5,5),(6,6),(1,3),(3,1),(1,5)、(5,1),(3,5),(5,3),(2,4),(4,2),(2,6),(6,2),(4,6),(6,4)共18个
事件AB,所包含的基本事件有:(2,2),(4,4),(6,6),(2,4),(4,2),(2,6),(6,2),(4,6),(6,4)共9个
根据条件概率公式P(B|A)=$\frac{{n}_{AB}}{{n}_{A}}$=$\frac{9}{18}=\frac{1}{2}$,
故选:D
点评 本题考查条件概率的计算公式,同时考查学生对基础知识的记忆、理解和熟练程度.属于基础题.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
12.某实验员在培养皿中滴入了含有10个某种真菌的实验液,经1小时培养真菌数目繁殖为原来的2倍.经测量知该真菌的繁殖规律为y=10eλt,其中λ为常数,t表示时间(单位:小时),y表示真菌个数.经过8小时培养,真菌能达到的个数为( )
| A. | 640 | B. | 1280 | C. | 2560 | D. | 5120 |
9.在等腰△ABC中,AB=AC,D是腰AC的中点,若sin∠CBD=$\frac{1}{4}$,则sin∠ABD=( )
| A. | $\frac{\sqrt{10}}{8}$ | B. | $\frac{\sqrt{6}}{4}$ | C. | $\frac{\sqrt{10}}{4}$ | D. | $\frac{\sqrt{6}}{8}$ |
6.若函数f(x)=x3-3x在区间[0,2]上有最大值m和最小值n,则m-n等于( )
| A. | -2 | B. | 0 | C. | 2 | D. | 4 |
3.若圆x2+y2+2x-6y+6=0有且仅有三个点到直线x+ay+1=0的距离为1,则实数a的值为( )
| A. | ±1 | B. | $±\frac{\sqrt{2}}{4}$ | C. | $±\sqrt{2}$ | D. | $±\frac{\sqrt{3}}{2}$ |
7.从装有2个红球和2个白球的袋内任取2个球,那么互斥而不对立的两个事件是( )
| A. | 至少有1个红球,都是红球 | B. | 恰有1个红球,恰有1个白球 | ||
| C. | 至少有1个红球,都是白球 | D. | 恰有1个白球,恰有2个白球 |
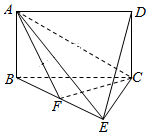 如图,四边形ABCD是矩形,平面ABCD⊥平面BCE,BE⊥EC.
如图,四边形ABCD是矩形,平面ABCD⊥平面BCE,BE⊥EC.