题目内容
8.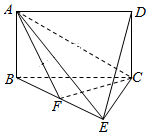 如图,四边形ABCD是矩形,平面ABCD⊥平面BCE,BE⊥EC.
如图,四边形ABCD是矩形,平面ABCD⊥平面BCE,BE⊥EC.(1)求证:平面AEC⊥平面ABE;
(2)点F在BE上,若DE∥平面ACF,DC=CE=$\frac{1}{2}$BC=3,求三棱锥A-BCF的体积.
分析 (1)根据平面ABCD⊥平面BCE,利用面面垂直的性质可得AB⊥平面BCE,从而可得CE⊥AB,由CE⊥BE,根据线面垂直的判定可得CE⊥平面ABE,从而可得平面AEC⊥平面ABE;
(2)连接BD交AC于点O,连接OF.根据DE∥平面ACF,可得DE∥OF,根据O为BD中点,可得F为BE中点,由已知求出底面三角形BCF的面积,代入体积公式得答案.
解答 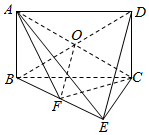 (1)证明:∵ABCD为矩形,∴AB⊥BC.
(1)证明:∵ABCD为矩形,∴AB⊥BC.
∵平面ABCD⊥平面BCE,平面ABCD∩平面BCE=BC,AB?平面ABCD,
∴AB⊥平面BCE.
∵CE?平面BCE,∴CE⊥AB.
∵CE⊥BE,AB?平面ABE,BE?平面ABE,AB∩BE=B,
∴CE⊥平面ABE.
∵CE?平面AEC,∴平面AEC⊥平面ABE.
(2)解:连接BD交AC于点O,连接OF.
∵DE∥平面ACF,DE?平面BDE,平面ACF∩平面BDE=OF,
∴DE∥OF.
又∵矩形ABCD中,O为BD中点,
∴F为BE中点,即BF=FE.
在Rt△BEC中,∵BC=6,EC=3,∴BE=$\sqrt{{6}^{2}-{3}^{2}}=3\sqrt{3}$.
∴${S}_{△AFC}=\frac{1}{2}×\frac{1}{2}×3\sqrt{3}×3=\frac{9\sqrt{3}}{4}$.
又AB=DC=3.
∴${V}_{A-BCF}=\frac{1}{3}×\frac{9\sqrt{3}}{4}×3=\frac{9\sqrt{3}}{4}$.
点评 本题考查面面垂直的判定,考查了棱锥体积的求法,考查空间想象能力和思维能力,是中档题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
18.现抛掷两枚骰子,记事件A为“朝上的2个数之和为偶数”,事件B为“朝上的2个数均为偶数”,则P(B|A)=( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{2}$ |
3.直线$\frac{x}{3}$-$\frac{y}{4}$=1在x轴上的截距是( )
| A. | -3 | B. | 3 | C. | -4 | D. | 4 |
13.下列函数中,既是偶函数又在区间 (0,+∞)上单调递减的是( )
| A. | y=$\frac{1}{x}$ | B. | y=e-x | C. | y=-x2+1 | D. | y═lg|x| |
13.已知{an}为等比数列,a4+a7=2,a2a9=-8,则a1+a10=( )
| A. | 7 | B. | 5 | C. | -7 | D. | -5 |
14.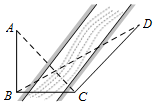 如图,某人为测量河对岸塔AB的高,先在塔底B的正东方向上的河岸上选一点C,在点C处测得点A的仰角为45°,并在点C北偏东15°方向的河岸上选定一点D,测得CD的距离为20米,∠BDC=30°,则塔AB的高是( )
如图,某人为测量河对岸塔AB的高,先在塔底B的正东方向上的河岸上选一点C,在点C处测得点A的仰角为45°,并在点C北偏东15°方向的河岸上选定一点D,测得CD的距离为20米,∠BDC=30°,则塔AB的高是( )
 如图,某人为测量河对岸塔AB的高,先在塔底B的正东方向上的河岸上选一点C,在点C处测得点A的仰角为45°,并在点C北偏东15°方向的河岸上选定一点D,测得CD的距离为20米,∠BDC=30°,则塔AB的高是( )
如图,某人为测量河对岸塔AB的高,先在塔底B的正东方向上的河岸上选一点C,在点C处测得点A的仰角为45°,并在点C北偏东15°方向的河岸上选定一点D,测得CD的距离为20米,∠BDC=30°,则塔AB的高是( )| A. | 10米 | B. | $10\sqrt{2}$米 | C. | $10\sqrt{3}$米 | D. | $20\sqrt{3}$米 |