题目内容
10.已知从圆C:(x+1)2+(y-2)2=2外一点P(x1,y1)向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,则当|PM|取最小值时点P的坐标为(-$\frac{3}{10}$,$\frac{3}{5}$).分析 ⊙C:x2+y2+2x-4y+3=0,化为标准方程,求出圆心C,半径r.设P(x,y).由切线的性质可得:CM⊥PM,利用|PM|=|PO|,可得2x1-4y1+3=0.要使|PM|最小,只要|PO|最小即可.
解答 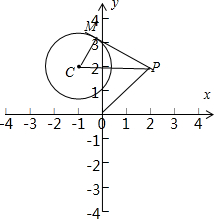 解:如图所示,⊙C:x2+y2+2x-4y+3=0化为(x+1)2+(y-2)2=2,圆心C(-1,2),半径r=$\sqrt{2}$.
解:如图所示,⊙C:x2+y2+2x-4y+3=0化为(x+1)2+(y-2)2=2,圆心C(-1,2),半径r=$\sqrt{2}$.
因为|PM|=|PO|,
所以|PO|2+r2=|PC|2(C为圆心,r为圆的半径),
所以x12+y12+2=(x1+1)2+(y1-2)2,即2x1-4y1+3=0.要使|PM|最小,只要|PO|最小即可.
当直线PO垂直于直线2x-4y+3=0时,即直线PO的方程为2x+y=0时,|PM|最小,此时P点即为两直线的交点,得P点坐标(-$\frac{3}{10}$,$\frac{3}{5}$).
故答案为(-$\frac{3}{10}$,$\frac{3}{5}$).
点评 本题考查了圆的切线的性质、勾股定理、两点之间的距离公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
20.已知函数f(x)=cos(2x-φ)-$\sqrt{3}$sin(2x-φ)(|φ|<$\frac{π}{2}$)的图象向右平移$\frac{π}{12}$个单位后关于y轴对称,则f(x)在区间$[{-\frac{π}{2},0}]$上的最小值为( )
| A. | -1 | B. | $\sqrt{3}$ | C. | $-\sqrt{3}$ | D. | -2 |
18.已知x,y满足约束条件$\left\{{\begin{array}{l}{x≤-1}\\{x-y≥-2}\\{x+y+1≥0}\end{array}}\right.$,则目标函数z=3x+y的取值范围为( )
| A. | [-4,-2] | B. | [-4,+∞) | C. | [-3,+∞) | D. | [-3,-2] |
2.集合A={x|x2-2x<0},B={x||x|<2},则( )
| A. | A∩B=∅ | B. | A∩B=A | C. | A∪B=A | D. | A∪B=R |
1.已知i为虚数单位,m∈R,复数z=(-m2+2m+8)+(m2-8m)i,若z为负实数,则m的取值集合为( )
| A. | {0} | B. | {8} | C. | (-2,4) | D. | (-4,2) |