Question

15．已知关于x的方程sinx+cosx=m在[0，π]有两个不等的实根，则m的一个值是（　　）

• A． 0
• B． $\frac{1}{2}$
• C． $\frac{\sqrt{2}}{2}$
• D． 1

Answer 1

分析 由于x的方程sinx+cosx=m得到$\sqrt{2}$sin（x+$\frac{π}{4}$）=m，分别画出y=$\sqrt{2}$sin（x+$\frac{π}{4}$），x∈[0，π]，和y=m，的图象，由图象可得答案

解答 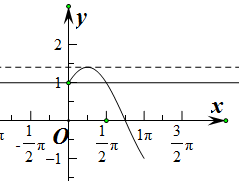解：于x的方程sinx+cosx=m在[0，π]有两个不等的实根，
则$\sqrt{2}$sin（x+$\frac{π}{4}$）=m，
分别画出y=$\sqrt{2}$sin（x+$\frac{π}{4}$），x∈[0，π]，和y=m，
由图象可得，若关于x的方程sinx+cosx=m在[0，π]有两个不等的实根，
则m的范围为[1，$\sqrt{2}$），
故选：A

点评 本题主要考查两角和差的正弦公式、正弦函数的值域，属于基础题．