题目内容
20．设函数f（x）=$\left\{\begin{array}{l}{{2}^{-x}，x＜1}\\{lo{g}_{2}x，x≥1}\end{array}\right.$，若函数y=f（x）-k有且只有两个零点，则实数k的取值范围是（$\frac{1}{2}$，+∞）．分析 根据题意，分析可得若函数y=f（x）-k有且只有两个零点，则函数y=f（x）的图象与直线y=k有且只有两个交点；作出函数y=f（x）的图象，分析直线y=k与其图象有且只有两个交点时k的取值范围，即可得答案．
解答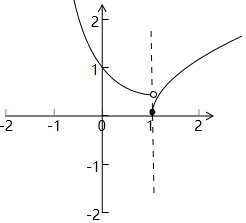 
解：根据题意，若函数y=f（x）-k有且只有两个零点，
则函数y=f（x）的图象与直线y=k有且只有两个交点，
而函数f（x）=$\left\{\begin{array}{l}{{2}^{-x}，x＜1}\\{lo{g}_{2}x，x≥1}\end{array}\right.$，其图象如图，
若直线y=k与其图象有且只有两个交点，必有k＞$\frac{1}{2}$，即实数k的取值范围是（$\frac{1}{2}$，+∞）；
故答案为：（$\frac{1}{2}$，+∞）．
点评 本题考查函数零点的判断方法，关键是将函数零点的个数转化为函数图象的交点个数的问题．
练习册系列答案
相关题目
12．在四棱锥P-ABCD中，PA⊥底面ABCD，其中PA=2AB=2AD=2，G为三角形BCD的重心，则PG与底面ABCD所成角的正弦值为（ ）
| A． | $3\sqrt{2}$ | B． | $\frac{3\sqrt{11}}{11}$ | C． | $\frac{{\sqrt{19}}}{19}$ | D． | $\frac{{3\sqrt{19}}}{19}$ |
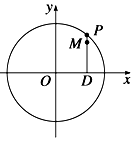如图，设P是圆x2+y2=6上的动点，点D是P在x轴上的投影，M为PD上一点，且$\overrightarrow{DP}=\sqrt{2}\overrightarrow{DM}$．
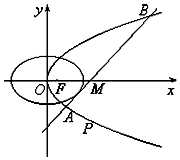如图所示，已知椭圆C1和抛物线C2有公共焦点F（1，0），C1的中心和C2的顶点都在坐标原点O，过点，M（4，0）的直线l与抛物线C2分别相交于A，B两点．