题目内容
18.曲线y=$\frac{2}{x}$与直线y=x-1及x=4所围成的封闭图形的面积为( )| A. | 2ln 2 | B. | 2-ln 2 | C. | 4-ln 2 | D. | 4-2ln 2 |
分析 先联立两个曲线的方程,求出交点,以确定积分公式中x的取值范围,最后根据定积分的几何意义表示出区域的面积,根据定积分公式解之即可.先联立两个曲线的方程,求出交点,以确定积分公式中x的取值范围,最后根据定积分的几何意义表示出区域的面积,根据定积分公式解之即可.
解答 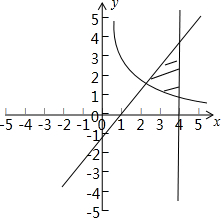 解:由曲线y=$\frac{2}{x}$与直线y=x-1联立,解得,x=-1,x=2,
解:由曲线y=$\frac{2}{x}$与直线y=x-1联立,解得,x=-1,x=2,
故所求图形的面积为S=${∫}_{2}^{4}$(x-1-$\frac{2}{x}$)dx=($\frac{1}{2}$x2-x-2lnx)|${\;}_{2}^{4}$=4-2ln2.
故选:C.
点评 本题主要考查了定积分在求面积中的应用,以及定积分的计算,属于基础题.

练习册系列答案
相关题目
6.设有直线m,n和平面α,β,下列四个命题中,正确的是( )
| A. | 若m∥α,n∥α,则m∥n | B. | 若m?α,n?α,m∥β,l∥β,则α∥β | ||
| C. | 若α⊥β,m?α,则m⊥β | D. | 若α⊥β,m⊥β,m?α,则m∥α |
3.圆锥过轴的截面是( )
| A. | 圆 | B. | 等腰三角形 | C. | 矩形 | D. | 抛物线 |
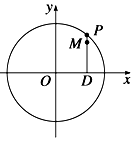 如图,设P是圆x2+y2=6上的动点,点D是P在x轴上的投影,M为PD上一点,且$\overrightarrow{DP}=\sqrt{2}\overrightarrow{DM}$.
如图,设P是圆x2+y2=6上的动点,点D是P在x轴上的投影,M为PD上一点,且$\overrightarrow{DP}=\sqrt{2}\overrightarrow{DM}$. 如图,在三棱柱ABC-A1B1C1中,面积为$\frac{9}{2}$的△ACB是等腰直角三角形且∠ACB=90°,C1B⊥面ABC,C1B=3.
如图,在三棱柱ABC-A1B1C1中,面积为$\frac{9}{2}$的△ACB是等腰直角三角形且∠ACB=90°,C1B⊥面ABC,C1B=3.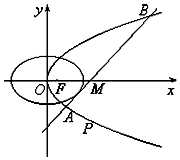 如图所示,已知椭圆C1和抛物线C2有公共焦点F(1,0),C1的中心和C2的顶点都在坐标原点O,过点,M(4,0)的直线l与抛物线C2分别相交于A,B两点.
如图所示,已知椭圆C1和抛物线C2有公共焦点F(1,0),C1的中心和C2的顶点都在坐标原点O,过点,M(4,0)的直线l与抛物线C2分别相交于A,B两点.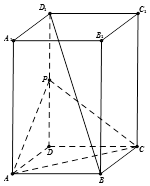 .如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
.如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.