题目内容
已知各项为正数的等比数列数列{an}的前n项和为Sn,数列{bn}的通项公式bn=
(n∈N*),若S3=b5+1,b4是a2和a4的等比中项.
(1)求数列{an}的通项公式;
(2)求数列{an•bn}的前n项和为Tn.
|
(1)求数列{an}的通项公式;
(2)求数列{an•bn}的前n项和为Tn.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)由已知得b5=6,b4=4,a1+a1q+a1q2=7,a2•a4=a32=16,从而q=2,a1=1,由此能求出数列{an}的通项公式.
(2)当n为偶数时,利用分组求和法和错位相减法能求出Tn=(n-1)•2n+1+
=(n-
)•2n+
.当n为奇数,且n≥3时,Tn=Tn-1+(n+1)•2n-1=(n-
)•2n-1+
+(n+1)•2n-1=(2n-
)•2n-1+
,由此能求出Tn.
(2)当n为偶数时,利用分组求和法和错位相减法能求出Tn=(n-1)•2n+1+
1-4
| ||
| 1-4 |
| 2 |
| 3 |
| 2 |
| 3 |
| 5 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
解答:
解:(1)∵数列{bn}的通项公式bn=
(n∈N*),
∴b5=6,b4=4,
设各项为正数的等比数列数列{an}的公比为q,q>0,
∵S3=b5+1=7,∴a1+a1q+a1q2=7,①
∵b4是a2和a4的等比中项,
∴a2•a4=a32=16,解得a3=a1q2=4,②
由①②得3q2-4q-4=0,
解得q=2,或q=-
(舍),
∴a1=1,an=2n-1.
(2)当n为偶数时,
Tn=(1+1)•20+2•2+(3+1)•22+4•23+(5+1)•24+…+[(n-1)+1]•2n-2+n•2n-1
=(20+2•2+3•22+4•23+…+n•2n-1)+(20+22+…+2n-2),
设Hn=20+2•2+3•22+4•23+…+n•2n-1,①
2Hn=2+2•22+3•23+4•24+…+n•2n,②
①-②,得-Hn=20+2+22+23+…+2n-1-n•2n
=
-n•2n
=(1-n)•2n-1,
∴Hn=(n-1)•2n+1,
∴Tn=(n-1)•2n+1+
=(n-
)•2n+
.
当n为奇数,且n≥3时,
Tn=Tn-1+(n+1)•2n-1=(n-
)•2n-1+
+(n+1)•2n-1=(2n-
)•2n-1+
,
经检验,T1=2符合上式,
∴Tn=
.
|
∴b5=6,b4=4,
设各项为正数的等比数列数列{an}的公比为q,q>0,
∵S3=b5+1=7,∴a1+a1q+a1q2=7,①
∵b4是a2和a4的等比中项,
∴a2•a4=a32=16,解得a3=a1q2=4,②
由①②得3q2-4q-4=0,
解得q=2,或q=-
| 2 |
| 3 |
∴a1=1,an=2n-1.
(2)当n为偶数时,
Tn=(1+1)•20+2•2+(3+1)•22+4•23+(5+1)•24+…+[(n-1)+1]•2n-2+n•2n-1
=(20+2•2+3•22+4•23+…+n•2n-1)+(20+22+…+2n-2),
设Hn=20+2•2+3•22+4•23+…+n•2n-1,①
2Hn=2+2•22+3•23+4•24+…+n•2n,②
①-②,得-Hn=20+2+22+23+…+2n-1-n•2n
=
| 1-2n |
| 1-2 |
=(1-n)•2n-1,
∴Hn=(n-1)•2n+1,
∴Tn=(n-1)•2n+1+
1-4
| ||
| 1-4 |
| 2 |
| 3 |
| 2 |
| 3 |
当n为奇数,且n≥3时,
Tn=Tn-1+(n+1)•2n-1=(n-
| 5 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
经检验,T1=2符合上式,
∴Tn=
|
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,是中档题,解题时要认真审题,注意分类讨论思想、分组求和法和错位相减法的合理运用.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
设变量x,y满足|x-1|+|y-a|≤1,若2x+y的最大值是5,则实数a的值是( )
| A、2 | B、1 | C、0 | D、-1 |
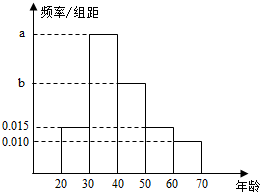 根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如图显示.
根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如图显示.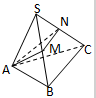 如图,△ABC外一点S,且SA⊥平面ABC,∠ABC=90°,AM⊥SB,AN⊥SC
如图,△ABC外一点S,且SA⊥平面ABC,∠ABC=90°,AM⊥SB,AN⊥SC