题目内容
求棱长为12的正四面体的体积.
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:先求出正四面体的底面积,正四面体的底面半径,再求出正四面体的高,由此能求出棱长为12的正四面体的体积.
解答:
解:正四面体的底面积为S=
×122×
=36
,
正四面体的底面半径为r=
×12×
=4
,
∴正四面体的高H=
=4
,
∴正四面体的体积为:
V=
SH=
×36
×4
=144
.
∴棱长为12的正四面体的体积为:144
.
| 1 |
| 2 |
| ||
| 2 |
| 3 |
正四面体的底面半径为r=
| ||
| 2 |
| 2 |
| 3 |
| 3 |
∴正四面体的高H=
122-(4
|
| 6 |
∴正四面体的体积为:
V=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 6 |
| 2 |
∴棱长为12的正四面体的体积为:144
| 2 |
点评:本题考查正四面体的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
 如图,在直角梯形ABCD中,∠BAD=∠ADC=90°,AB<CD,PD⊥平面ABCD,AB=AD=a,PD=
如图,在直角梯形ABCD中,∠BAD=∠ADC=90°,AB<CD,PD⊥平面ABCD,AB=AD=a,PD=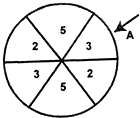 如图,一个圆形游戏转盘被分成6个均匀的扇形区域.用力旋转转盘,转盘停止转动时,箭头A所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头A指向每个区域的可能性都是相等的.在一次家庭抽奖的活动中,要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘,得分情况记为(a,b)(假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).
如图,一个圆形游戏转盘被分成6个均匀的扇形区域.用力旋转转盘,转盘停止转动时,箭头A所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头A指向每个区域的可能性都是相等的.在一次家庭抽奖的活动中,要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘,得分情况记为(a,b)(假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).