Question

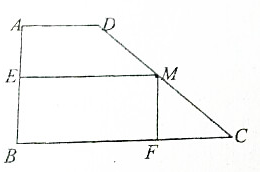如图，有一块形状为直角梯形的木板ABCD，AD∥BC，∠B是直角，AD=m，且AD：AB：BC=1：2：3，现从中截取一块矩形木板EBFM，使点E，F，M分别落在AB，BC，CD边上，设矩形的高FM=x，矩形的面积为y．
（1）求y关于x的函数关系式，并指出定义域；
（2）求x值，使矩形面积最大，并求矩形面积的最大值．

Answer 1

考点：函数解析式的求解及常用方法,函数的最值及其几何意义

专题：函数的性质及应用

分析：（1）根据已知条件容易求出AB=2m，BC=3m，∠BCD=45°，所以矩形的面积y=（3m-x）x，并且定义域为（0，2m）；
（2）对矩形的面积的解析式配方得y=-(x-

3m

2

)2+

9m2

4

，所以可以看出x=

3m

2

时，y取到最大值

9m2

4

．

解答： 解：（1）由已知条件得AB=2m，BC=3m，∠BCD=45°，BF=3m-x，0＜x＜2m；
∴y=（3m-x）x=-x²+3mx；
即：y=-x²+3mx，定义域为（0，2m）；
（2）y=-x2+3mx=-(x-

3m

2

)2+

9m2

4

；
∴x=

3m

2

时，矩形面积取最大值

9m2

4

．

点评：考查根据实际问题求函数解析式的方法，以及配方法求二次函数的最大值．