题目内容
已知函数f(x)=ax2+bx.
(1)试用f(1),f(-1)表示函数f(x);
(2)若1≤f(-1)≤2,2≤f(1)≤4,求f(-2)的取值范围.
(1)试用f(1),f(-1)表示函数f(x);
(2)若1≤f(-1)≤2,2≤f(1)≤4,求f(-2)的取值范围.
考点:函数解析式的求解及常用方法,函数的值
专题:计算题,函数的性质及应用
分析:(1)由题意可得f(1)=a+b,f(-1)=a-b,从而求函数f(x);
(2)由题意,f(-2)=2[f(1)+f(-1)]-[f(1)-f(-1)]=3f(-1)+f(1),从而求得.
(2)由题意,f(-2)=2[f(1)+f(-1)]-[f(1)-f(-1)]=3f(-1)+f(1),从而求得.
解答:
解:(1)根据函数解析式知f(1)=a+b,f(-1)=a-b,
解得a=
,b=
,
故f(x)=
x2+
x.
(2)根据(1),
f(-2)=2[f(1)+f(-1)]-[f(1)-f(-1)]=3f(-1)+f(1),
又1≤f(-1)≤2,2≤f(1)≤4,
所以5≤3f(-1)+f(1)≤10,
即5≤f(-2)≤10.
解得a=
| f(1)+f(-1) |
| 2 |
| f(1)-f(-1) |
| 2 |
故f(x)=
| f(1)+f(-1) |
| 2 |
| f(1)-f(-1) |
| 2 |
(2)根据(1),
f(-2)=2[f(1)+f(-1)]-[f(1)-f(-1)]=3f(-1)+f(1),
又1≤f(-1)≤2,2≤f(1)≤4,
所以5≤3f(-1)+f(1)≤10,
即5≤f(-2)≤10.
点评:本题考查了函数的定义及应用,属于基础题.

练习册系列答案
相关题目
解关于x的不等式
≥2,所得的解集为( )
| 3x+2 |
| x+1 |
| A、{x|x>0或x≤-1} |
| B、{x|-1<x≤0} |
| C、{x|x≥0或x<-1} |
| D、{x|-1<x<0} |
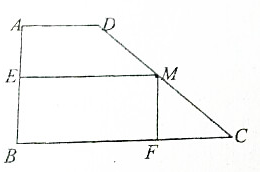 如图,有一块形状为直角梯形的木板ABCD,AD∥BC,∠B是直角,AD=m,且AD:AB:BC=1:2:3,现从中截取一块矩形木板EBFM,使点E,F,M分别落在AB,BC,CD边上,设矩形的高FM=x,矩形的面积为y.
如图,有一块形状为直角梯形的木板ABCD,AD∥BC,∠B是直角,AD=m,且AD:AB:BC=1:2:3,现从中截取一块矩形木板EBFM,使点E,F,M分别落在AB,BC,CD边上,设矩形的高FM=x,矩形的面积为y.