题目内容
已知f(x)=-x3-ax在(-∞,-1]上递减,且g(x)=2x-
在区间(1,2]上既有最大值又有最小值,则a的取值范围是( )
| a |
| x |
| A、a>-2 |
| B、a≥-3 |
| C、-3≤a<-2 |
| D、-3≤a≤-2 |
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:求出函数的导数,利用导数小于等于0,求出a的范围,通过最值即可求解.
解答:
解:由f'(x)=-3x2-a≤0对于一切x∈(-∞,-1]恒成立,得-3x2≤a,∴a≥-3.
又由g(x)=2x-
,可知g′(x)=2+
在 (1,2]上有零点,也就是极值点,2+
=0,解得a=-2x2,
在 (1,2]上有最大最小值,知-8≤a<-2,∴-3≤a<-2.
故选:C.
又由g(x)=2x-
| a |
| x |
| a |
| x2 |
| a |
| x2 |
在 (1,2]上有最大最小值,知-8≤a<-2,∴-3≤a<-2.
故选:C.
点评:本题考查函数的导数的综合应用,单调性以及函数的最值,考查转化思想以及计算能力.

练习册系列答案
相关题目
甲:函数f(x)是奇函数;乙:函数f(x)在定义域上是增函数.对于函数①f(x)=tan x,②f(x)=-
,③f(x)=x|x|,能使甲、乙均为真命题的所有函数的序号是( )
| 1 |
| x |
| A、①② | B、②③ | C、③ | D、①②③ |
如图为一个求20个数的平均数的程序,在横线上应填充的是 ( )


| A、i>20 | B、i<20 |
| C、i>=20 | D、i<=20 |
将表的分针拨快(顺时针)10分钟,则分针旋转过程中形成的角的弧度数是( )
A、
| ||
B、
| ||
C、-
| ||
D、-
|
设集合A={x|1<x<2},B={x|x<a},且A⊆B,则实数a的范围( )
| A、a≥2 | ||
| B、a>2 | ||
| C、a≤1 | ||
D、0<x≤
|
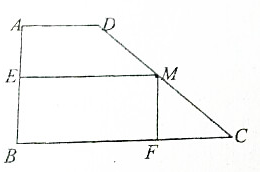 如图,有一块形状为直角梯形的木板ABCD,AD∥BC,∠B是直角,AD=m,且AD:AB:BC=1:2:3,现从中截取一块矩形木板EBFM,使点E,F,M分别落在AB,BC,CD边上,设矩形的高FM=x,矩形的面积为y.
如图,有一块形状为直角梯形的木板ABCD,AD∥BC,∠B是直角,AD=m,且AD:AB:BC=1:2:3,现从中截取一块矩形木板EBFM,使点E,F,M分别落在AB,BC,CD边上,设矩形的高FM=x,矩形的面积为y.