题目内容
已知a∈(
,π),sin
-cos
=
,则cosa=( )
| π |
| 2 |
| a |
| 2 |
| a |
| 2 |
| ||
| 5 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
考点:二倍角的余弦
专题:计算题,三角函数的求值
分析:原式两边平方可解得sina=-
,由a∈(
,π),即可计算cosa的值.
| 3 |
| 5 |
| π |
| 2 |
解答:
解:∵sin
-cos
=
,
∴两边平方可得:1+sina=
,即sina=-
∵a∈(
,π),
∴cosa=-
=-
故选:A.
| a |
| 2 |
| a |
| 2 |
| ||
| 5 |
∴两边平方可得:1+sina=
| 2 |
| 5 |
| 3 |
| 5 |
∵a∈(
| π |
| 2 |
∴cosa=-
| 1-sin2α |
| 4 |
| 5 |
故选:A.
点评:本题主要考察了二倍角的余弦公式的应用,属于基本知识的考查.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
解关于x的不等式
≥2,所得的解集为( )
| 3x+2 |
| x+1 |
| A、{x|x>0或x≤-1} |
| B、{x|-1<x≤0} |
| C、{x|x≥0或x<-1} |
| D、{x|-1<x<0} |
如图为一个求20个数的平均数的程序,在横线上应填充的是 ( )


| A、i>20 | B、i<20 |
| C、i>=20 | D、i<=20 |
将表的分针拨快(顺时针)10分钟,则分针旋转过程中形成的角的弧度数是( )
A、
| ||
B、
| ||
C、-
| ||
D、-
|
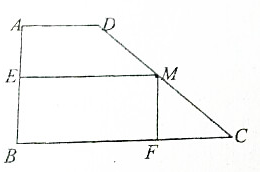 如图,有一块形状为直角梯形的木板ABCD,AD∥BC,∠B是直角,AD=m,且AD:AB:BC=1:2:3,现从中截取一块矩形木板EBFM,使点E,F,M分别落在AB,BC,CD边上,设矩形的高FM=x,矩形的面积为y.
如图,有一块形状为直角梯形的木板ABCD,AD∥BC,∠B是直角,AD=m,且AD:AB:BC=1:2:3,现从中截取一块矩形木板EBFM,使点E,F,M分别落在AB,BC,CD边上,设矩形的高FM=x,矩形的面积为y.