题目内容

给出下列三个命题：
①函数y=
1
2
ln
1-cosx
1+cosx
与y=lntan
x
2
是同一函数．
②已知随机变量X服从正态分布N（1，σ2），若P（x≤2）=0.72，则P（x≤0）=0.28．
③如图，在△ABC中，
AN
=
1
3
NC
，P是BN上的一点，若
AP
=m
AB
+
2
11
AC
，则实数m的值为
3
11
．
其中真命题是
 
．（写出所有真命题的序号）
考点：命题的真假判断与应用
专题：探究型
分析：对于①中的两个函数定义域不同，故不是同一个函数．
对于②，根据正态分布的计算公式，计算证明是正确的
对于③，根据平面向量的基本定理，求出m 的值即可
解答： 解：对于①，∵y=
1
2
ln
1-cosx
1+cosx
，定义域应为
1-cosx
1+cosx
＞0，
只要1+cosx≠0，∴cosx≠-1，∴x≠2kπ
对于y=lntan
x
2
，定义域应为tan
x
2
＞0，∴kπ＜
x
2
＜kπ+
π
2

因此，两个函数定义域不同，故不是同一个函数．①是不准确的
对于②，∵X～N（1，σ2），且P（x≤2）=0.72，
∴P（x≥0）=p（x＞2）=1-0.72=0.28，因此，②正确
对于③，设
BP
=λ
BN
，则
AP
=
AB
+
BP
=
AB
+λ
BN
=
AB
+λ（
AN
-
AB
）=（1-λ）
AB
+λ
AN
=（1-λ）
AB
+
λ
3
AC

 又∵
AP
=m
AB
+
2
11
AC
，根据平面向量基本定理，得
1-λ=m
2
11
=
λ
3
，
∴λ=
6
11

故答案：②③
点评：①考查了相同函数的定义，②考查了正态分布的概率计算，③考查了平面向量基本定理的应用
练习册系列答案
相关题目
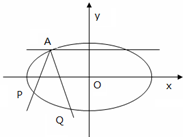如图，焦点在x轴的椭圆，离心率e=
2
2
，且过点A（-2，1），由椭圆上异于点A的P点发出的光线射到A点处被直线y=1反射后交椭圆于Q点（Q点与P点不重合）．
（1）求椭圆标准方程；
（2）求证：直线PQ的斜率为定值；
（3）求△OPQ的面积的最大值．
给出四个命题：其中所有的正确命题的序号是
 

①存在实数α，使sinαcosα=1；
②存在实数α，使sinα+cosα=
3
2
；
③y=sin(
5π
2
-2x)是偶函数；
④x=
π
8
是函数y=sin(2x+
5π
4
)的一条对称轴方程；
⑤若α，β是第一象限角，且α＞β，则sinα＞sinβ．
∫
1
-1
sinxdx=
 
．
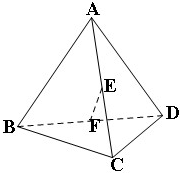如图是将边长为2，有一内角为60°的菱形ABCD沿较短对角线BD折成四面体ABCD，点E、F分别为AC、BD的中点，则下列命题中正确的是
 
．（将正确的命题序号全填上）．
①EF∥AB；
②当二面角A-BD-C的大小为60°时，AC=2；
③当四面体ABCD的体积最大时，AC=
6
；
④AC垂直于截面BDE．
如图所示，f（x）是定义在区间[-c，c]（c＞0）上的奇函数，令g（x）=af（x）+b，并有关于函数g（x）的四个论断：
①若a＞0，对于[-1，1]内的任意实数m，n（m＜n），
g(n)-g(m)
n-m
＞0恒成立；
②函数g（x）是奇函数的充要条件是b=0；
③任意a∈R，g（x）的导函数g′（x）有两个零点；
④若a≥1，b＜0，则方程g（x）=0必有3个实数根；
其中，所有正确结论的序号是
 
．
如图在四面体ABCD中，若截面PQMN是正方形，则在下列命题中正确的有
 
．（填上所有正确命题的序号） 
①AC⊥BD
②AC=BD
③AC∥截面PQMN
④异面直线PM与BD所成的角为45°．
在直角坐标系xOy中，圆C的参数方程为
x=-
2
+rcosθ
y=-
2
+rsinθ
（θ为参数，r＞0）．以O为极点，x轴正半轴为极轴，并取相同的单位长度建立极坐标系，直线l的极坐标方程为ρsin(θ+
π
4
)=1．当圆C上的点到直线l的最大距离为4时，圆的半径r=
 
．
下列说法正确的个数是（　　）
①空集是任何集合的真子集；②函数f（x）=3x+1是指数函数；③既是奇函数又是偶函数的函数有无数多个；④若A∪B=B，则A∩B=A．
A、0个B、1个C、2个D、3个

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网