题目内容
14.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1,F2,点P在椭圆上,O为坐标原点,若|OP|=$\frac{1}{2}$|F1F2|,且|PF1|•|PF2|=a2,则该椭圆的离心率为( )| A. | $\frac{3}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
分析 由椭圆的定义可得,|PF1|+|PF2|=2a,又|PF1|•|PF2|=a2,可得|PF1|=|PF2|=a,即P为椭圆的短轴的端点,由条件可得b=c,计算即可得到椭圆的离心率.
解答 解:由椭圆的定义可得,|PF1|+|PF2|=2a,
又|PF1|•|PF2|=a2,
可得|PF1|=|PF2|=a,即P为椭圆的短轴的端点,
|OP|=b,且|OP|=$\frac{1}{2}$|F1F2|=c,
即有c=b=$\sqrt{{a}^{2}-{c}^{2}}$,
即为a=$\sqrt{2}$c,e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$.
故选:C.
点评 本题考查椭圆的离心率的求法,注意运用椭圆的定义,以及a,b,c的关系,考查运算能力,属于基础题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
2.东莞某家具生产厂家根据市场调查分析,决定调整新产品生产方案,准备每周(按40个工时计算)生产书桌、书柜、电脑椅共120张,且书桌至少生产20张.已知生产这些家具每张所需工时和每张产值如表:
问每周应生产书桌、书柜、电脑椅各多少张,才能使产值最高?最高产值是多少?(以千元为单位)
| 家具名称 | 书桌 | 书柜 | 电脑椅 |
| 工 时 | $\frac{1}{2}$ | $\frac{1}{3}$ | $\frac{1}{4}$ |
| 产值(千元) | 4 | 3 | 2 |
3.运行如图所示的程序框图,则输出的数是7的倍数的概率为( )
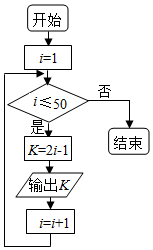

| A. | $\frac{4}{25}$ | B. | $\frac{8}{49}$ | C. | $\frac{7}{50}$ | D. | $\frac{14}{99}$ |
 已知椭圆$G:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的长轴长为$2\sqrt{2}$,离心率$e=\frac{{\sqrt{2}}}{2}$.
已知椭圆$G:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的长轴长为$2\sqrt{2}$,离心率$e=\frac{{\sqrt{2}}}{2}$.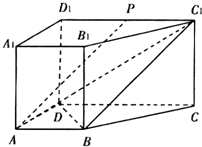 如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AD⊥AB,AB=AD=$\frac{1}{2}$CD=1.点P为线段C1D1的中点.
如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AD⊥AB,AB=AD=$\frac{1}{2}$CD=1.点P为线段C1D1的中点.