题目内容
8.已知数列{an}的前n项和Sn=3n+t(n∈N*),求证:t=-1是{an}为等比数列的充要条件.分析 由等比数列通项公式和前n项和公式的关系,分充分性和必要性两方面来证明可得.
解答 证明:(1)充分性:
当t=-1时,a1=S1=3-1=2.
当n≥2时,an=Sn-Sn-1=2×3n-1.
上式当n=1时也成立,∴$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{{2×3}^{n}}{2×{3}^{n-1}}$=3,
即数列{an}为等比数列.
(2)必要性:当n=1时,a1=S1=3+t.
当n≥2时,an=Sn-Sn-1=3n-1.
∴$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{{2×3}^{n}}{2×{3}^{n-1}}$=3
∵{an}为等比数列,
∴$\frac{{a}_{2}}{{a}_{1}}$=$\frac{3×2}{3+t}$=3,
∴t=-1.
综上所述,数列{an]为等比数列的充要条件是t=-1.
点评 本题考查等比数列的性质和应用,考查充要条件的证明,属中档题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
18.海上有相距10海里的A与B两个小岛,从A岛望另外一个C岛和B岛成60°的视角,从B岛望C岛和A岛成75°的视角,则B与C之间的距离是( )
| A. | $10\sqrt{3}$海里 | B. | $\frac{{10\sqrt{6}}}{3}$海里 | C. | $5\sqrt{2}$ 海里 | D. | $5\sqrt{6}$海里 |
19.在三角形中,角A,B,C的对边分别为a,b,c,若2sinAcosC=sinB,则$\frac{a}{c}$的值是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
13.函数f(x)=tanωx(ω>0)的图象的相邻两支截直线y=1所得的线段长为$\frac{π}{4}$,则f($\frac{π}{12}$)的值是( )
| A. | 0 | B. | $\frac{\sqrt{3}}{3}$ | C. | 1 | D. | $\sqrt{3}$ |
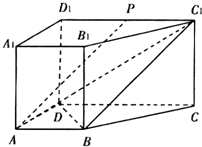 如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AD⊥AB,AB=AD=$\frac{1}{2}$CD=1.点P为线段C1D1的中点.
如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AD⊥AB,AB=AD=$\frac{1}{2}$CD=1.点P为线段C1D1的中点.