题目内容
17.解下列方程:(1)2x=$\sqrt{2}$;
(2)log2(3x)=log2(2x+1);
(3)2×5x+1-3=0.
分析 根指数函数和对数函数的性质,即可求出x的值.
解答 解:(1)2x=$\sqrt{2}$=${2}^{\frac{1}{2}}$,解得x=$\frac{1}{2}$;
(2)log2(3x)=log2(2x+1),则3x=2x+1,解得x=1,
(3)2×5x+1-3=0,解得x=log5$\frac{3}{2}$-1.
点评 本题考查了指数方程和对数方程,属于基础题.

练习册系列答案
相关题目
12.已知实数x、y满足条件:$\left\{\begin{array}{l}x-y-1≤0\\ 2x+y-4≥0\\ y≤2\end{array}\right.$,则$\frac{2x^2+y^2}{xy}$的最大值与最小值的和为( )
| A. | $\frac{20}{3}$ | B. | $\frac{42}{5}$+2$\sqrt{2}$ | C. | $\frac{136}{15}$ | D. | $\frac{27}{5}$+2$\sqrt{2}$ |
9.已知向量$\overrightarrow{OA}$,$\overrightarrow{OB}$满足|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,$\overrightarrow{OA}$⊥$\overrightarrow{OB}$,$\overrightarrow{OC}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$(λ,μ∈R),若M为线段AB的中点,并且|$\overrightarrow{MC}$|=1,则λ+μ的最大值为( )
| A. | 1+$\sqrt{2}$ | B. | 1-$\sqrt{2}$ | C. | $\sqrt{2}$-1 | D. | 1 |
7.在等差数列{an}中,已知a1=3,a9=11则前9项和S9=( )
| A. | 63 | B. | 65 | C. | 72 | D. | 62 |
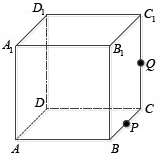 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是①③④⑤(写出所有正确命题的编号).
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是①③④⑤(写出所有正确命题的编号).