题目内容
2.椭圆$\frac{{x}^{2}}{4}$+y2=1的焦点为F1、F2,点P在椭圆上,如果线段PF1的中点在y轴上,那么|PF1|是|PF2|的( )| A. | 3倍 | B. | 4倍 | C. | 5倍 | D. | 7倍 |
分析 椭圆$\frac{{x}^{2}}{4}$+y2=1,a=2,b=1,|PF1|+|PF2=4.由线段PF1的中点E在y轴上,O为F1F2的中点,可得PF2∥OE.求出|PF2|=$\frac{{b}^{2}}{a}$=$\frac{1}{2}$,可得|PF1|.
解答 解:∵椭圆$\frac{{x}^{2}}{4}$+y2=1,∴a=2,b=1,|PF1|+|PF2=4.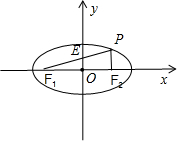
∵线段PF1的中点E在y轴上,O为F1F2的中点,
∴PF2∥OE.
∴|PF2|=$\frac{{b}^{2}}{a}$=$\frac{1}{2}$,|PF1|=4-$\frac{1}{2}$=$\frac{7}{2}$.
∴|PF1|=7|PF2|,
故选:D.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交弦长问题、三角形中位线定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
7.已知抛物线C:x2=2py(p>0)的焦点为F,直线x=4与x轴的交点为P,与C的交点为Q,且$|{QF}|=\frac{5}{4}|{PQ}|$,则抛物线C的方程为( )
| A. | x2=2y | B. | x2=4y | C. | x2=8y | D. | x2=16y |
11.已知a→=(-2,1),b→=(k,-3),c→=(1,2),若(a→-2b→)⊥c→,则|b→|=( )
| A. | 10 | B. | 35 | C. | 32 | D. | 25 |