题目内容
6.二次函数f(x)满足且f(0)=0,且对任意x∈R总有f(x+1)=f(x)+x+1,求f(x)的解析式.分析 f(x)是二次函数,设出解析式,利用待定系数法求解.
解答 解:由题意:f(x)是二次函数,设f(x)=ax2+bx+c,
∵f(0)=0,
∴c=0,
则f(x)=ax2+bx,
∵f(x+1)=f(x)+x+1,即a(x+1)2+b(x+1)=ax2+x(b+1)+1
由:$\left\{\begin{array}{l}{2a+b=b+1}\\{a+b=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=\frac{1}{2}}\end{array}\right.$.
故得f(x)的解析式为:f(x)=$\frac{1}{2}$x2+$\frac{1}{2}$x+c,
点评 本题考查了函数解析式的求法,利用了利用待定系数法,属于基础题.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
1.已知2x1+1,2x2+1,2x3+1,…,2xn+1的方差是3,则x1,x2,x3,…,xn的标准差为( )
| A. | $\frac{3}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 3 | D. | $\sqrt{3}$ |
11.已知a→=(-2,1),b→=(k,-3),c→=(1,2),若(a→-2b→)⊥c→,则|b→|=( )
| A. | 10 | B. | 35 | C. | 32 | D. | 25 |
15.设全集U是实数集R,M={x∈Z|-2≤x≤2},N={x∈N|-1<x≤4},则图中阴影部分所表示的集合是( ) 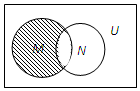

| A. | {-2,-1} | B. | {0,1,2} | C. | {-2,-1,3} | D. | {-2,-1,0} |
 已知函数f(x)=1+$\frac{x-|x|}{4}$.
已知函数f(x)=1+$\frac{x-|x|}{4}$.