题目内容
已知向量
、
、
满足|
|=|
|=3,
•
=
,|
-
-
|=1,则|
|的最大值为 .
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| 3 |
| 2 |
| c |
| a |
| b |
| c |
考点:平面向量数量积的运算,向量的模
专题:平面向量及应用
分析:本题可利用条件|
-
-
|=1,将(
+
)看成一个整体,得到关于|
|的一个不等式,再利用题中条件求出|
+
|,从而得到本题结论.
| c |
| a |
| b |
| a |
| b |
| c |
| a |
| b |
解答:
解:∵|
|=|
|=3,
•
=
,
∴|
+
|2=(|
|+
|)2=|
|2+|
|2+2
•
=21,
∴|
+
|=
.
∵|
-
-
|=1,
∴|
|-|
+
|≤|
-(
+
)|≤1,
∴|
|≤1+|
+
|=
+1.
故答案为:
+1.
| a |
| b |
| a |
| b |
| 3 |
| 2 |
∴|
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
∴|
| a |
| b |
| 21 |
∵|
| c |
| a |
| b |
∴|
| c |
| a |
| b |
| c |
| a |
| b |
∴|
| c |
| a |
| b |
| 21 |
故答案为:
| 21 |
点评:本题考查了模平方的计算公式和模的不等式,本题运算量不大,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知定义在R上的偶函数f(x)满足f(x-1)=f(x+1),当0≤x≤1时,f(x)=x2,如果函数g(x)=f(x)-(x+m)有两个零点,则实数m的值为( )
| A、2k(k∈Z) | ||
B、2k-
| ||
C、2K或2K+
| ||
D、2K或2K-
|
“m=-2”是“直线mx+2y+2=0与直线2x+my+2=0平行”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
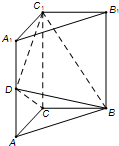 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=