题目内容
在数列{an}中,a1=1,且满足an-an-1=n(n>1).
(Ⅰ)求a2,a3及数列{an}的通项公式;
(Ⅱ)设bn=
,求数列{bn}的前n项和Sn.
(Ⅰ)求a2,a3及数列{an}的通项公式;
(Ⅱ)设bn=
| 1 |
| an |
考点:数列的求和,数列递推式
专题:综合题,等差数列与等比数列
分析:(Ⅰ)利用数列{an}中,a1=1,且满足an-an-1=n,代入计算,可得a2,a3;利用叠加法,求出数列{an}的通项公式;
(Ⅱ)利用裂项求和,即可求数列{bn}的前n项和Sn.
(Ⅱ)利用裂项求和,即可求数列{bn}的前n项和Sn.
解答:
解:(Ⅰ)∵数列{an}中,a1=1,且满足an-an-1=n,
∴a2=3,a3=5,
由an-an-1=n,
可知a2-a1=2,
a3-a2=3,
…
an-an-1=n;
当n≥2时,将上面各等式相加,得an-a1=2+…+n=
∴数列{an}的通项公式an=
+1=
;
(Ⅱ)bn=
=2(
-
),
∴数列{bn}的前n项和Sn=
(1-
+
-
+…+
-
)=
.
∴a2=3,a3=5,
由an-an-1=n,
可知a2-a1=2,
a3-a2=3,
…
an-an-1=n;
当n≥2时,将上面各等式相加,得an-a1=2+…+n=
| (n-1)(n+2) |
| 2 |
∴数列{an}的通项公式an=
| (n-1)(n+2) |
| 2 |
| n(n+1) |
| 2 |
(Ⅱ)bn=
| 1 |
| an |
| 1 |
| n |
| 1 |
| n+1 |
∴数列{bn}的前n项和Sn=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| n |
| 2(n+1) |
点评:本题考查了等差数列的基本知识,累和法求通项公式,裂项求和,考查了学生的计算能力,解题时要认真审题,仔细解答,避免错误,属于中档题.

练习册系列答案
相关题目
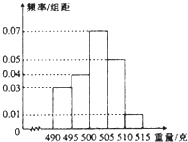 某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的N件产品作为样本称出它们的重量(单位;克),重量的分组区间为(490,495],(495,500],…(510,515],由此得到样本的频率分布直方图,如图所示,若其中重量超过510克的产品件数为3.
某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的N件产品作为样本称出它们的重量(单位;克),重量的分组区间为(490,495],(495,500],…(510,515],由此得到样本的频率分布直方图,如图所示,若其中重量超过510克的产品件数为3.