题目内容
6.下边是高中数学常用逻辑用语的知识结构图,则(1)、(2)处依次为( )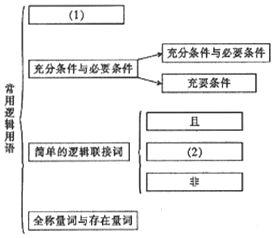
| A. | 命题及其关系、或 | B. | 命题的否定、或 | C. | 命题及其关系、并 | D. | 命题的否定、并 |
分析 命题的否定在全称量词与存在量词这一节中,简单的逻辑联结词包括或、且、非,可得结论.
解答 解:命题的否定在全称量词与存在量词这一节中,简单的逻辑联结词包括或、且、非,
故选A.
点评 本题考查知识结构图,知识结构图比较直观地描述了知识之间的关联,解题的关键是理解知识结构图的作用及知识之间的上下位关系.

练习册系列答案
相关题目
16.已知某学校有1680名学生,现在采用系统抽样的方法抽取84人,调查他们对学校食堂的满意程度,将1680人,按1,2,3,…,1680随机编号,则在抽取的84人中,编号落在[61,160]内的人数为( )
| A. | 7 | B. | 5 | C. | 3 | D. | 4 |
1.若函数f(x)=log2(x+a)与g(x)=x2-(a+1)x-4(a+5)存在相同的零点,则a的值为( )
| A. | 4或-$\frac{5}{2}$ | B. | 4或-2 | C. | 5或-2 | D. | 6或-$\frac{5}{2}$ |
11.已知定义在R上的函数f(x)满足f(x)=(x+2),且当-l≤x≤1时,f(x)=2|x|,函数g(x)=x+$\sqrt{2}$,实数a,b满足b>a>3.若?x1∈[a,b],?x2∈[-$\sqrt{2}$,0],使得f(x1)=g(x2)成立,则b-a的最大值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
18.已知P,A,B,C是球O球面上的四点,△ABC是正三角形,三棱锥P-ABC的体积为$\frac{9\sqrt{3}}{4}$,且∠APO=∠BPO=∠CPO=30°,则球O的表面积为( )
| A. | 4π | B. | $\frac{32}{3}$π | C. | 16π | D. | 12π |
15.已知点P(a,b)及圆O:x2+y2=r2,则“点P在圆O内”是“直线l:ax+by=r2与圆O相离”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |