题目内容
1.若函数f(x)=log2(x+a)与g(x)=x2-(a+1)x-4(a+5)存在相同的零点,则a的值为( )| A. | 4或-$\frac{5}{2}$ | B. | 4或-2 | C. | 5或-2 | D. | 6或-$\frac{5}{2}$ |
分析 求解方程x2-(a+1)x-4(a+5)=0,得到函数g(x)=x2-(a+1)x-4(a+5)的零点,代入方程log2(x+a)=0求得a值.
解答 解:由x2-(a+1)x-4(a+5)=0,解得x=-4或x=a+5.
∵函数f(x)=log2(x+a)与g(x)=x2-(a+1)x-4(a+5)存在相同的零点,
∴x=-4,x=a+5也是方程log2(x+a)=0的根.
即log2(-4+a)=0或log2(a+5+a)=0,
解得a=5或a=-2.
故选:C.
点评 本题考查函数零点的判定,考查对数方程的解法,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.已知底面是边长为2的正方形的四棱锥P-ABCD中,四棱锥的侧棱长都为4,E是PB的中点,则异面直线AD与CE所成角的余弦值为( )
| A. | $\frac{{\sqrt{6}}}{4}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
9.若抛物线y2=2px(p>0)的焦点在圆C:(x+2)2+y2=16上,则p的值为( )
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
6.下边是高中数学常用逻辑用语的知识结构图,则(1)、(2)处依次为( )
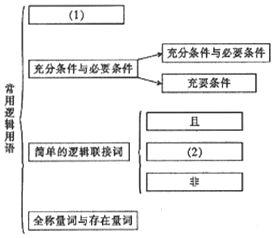

| A. | 命题及其关系、或 | B. | 命题的否定、或 | C. | 命题及其关系、并 | D. | 命题的否定、并 |
10.设函数f(x)=lnx-ax,g(x)=ex-3ax,其中a为实数,若f(x)在(1,+∞)上是单调减函数,且g(x)在(1,+∞)上有最小值,则a的取值范围是( )
| A. | ($\frac{e}{3}$,+∞) | B. | [$\frac{e}{3}$,+∞) | C. | (1,+∞) | D. | [1,+∞) |
11.已知经过点P(3,m)和点Q(m,-2)的直线的斜率等于2,则m的值为( )
| A. | $\frac{4}{3}$ | B. | 1 | C. | 2 | D. | -1 |