题目内容
14.若函数f(x)=sin(ωx+$\frac{π}{3}$)(0<ω<1)的图象关于点(-2,0)对称,则ω=$\frac{π}{6}$.分析 利用正弦函数的图象的对称性,可得-2•ω+$\frac{π}{3}$=kπ,由此求得ω的值.
解答 解:∵函数f(x)=sin(ωx+$\frac{π}{3}$)(0<ω<1)的图象关于点(-2,0)对称,
∴-2•ω+$\frac{π}{3}$=kπ,即ω=-$\frac{kπ}{2}$+$\frac{π}{6}$,k∈Z,∴ω=$\frac{π}{6}$,
故答案为:$\frac{π}{6}$.
点评 本题主要考查正弦函数的图象的对称性,属于基础题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
9.若抛物线y2=2px(p>0)的焦点在圆C:(x+2)2+y2=16上,则p的值为( )
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
19.若集合M={x|x2+5x-14<0},N={x|m<x<m+3},且M∩N=∅,则m的取值范围为( )
| A. | (-10,2) | B. | (-∞,-10)∪(2,+∞) | C. | [-10,2] | D. | (-∞,-10]∪[2,+∞) |
6.下边是高中数学常用逻辑用语的知识结构图,则(1)、(2)处依次为( )
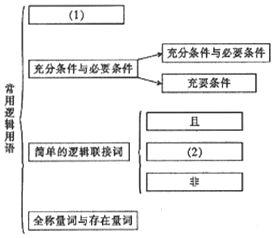

| A. | 命题及其关系、或 | B. | 命题的否定、或 | C. | 命题及其关系、并 | D. | 命题的否定、并 |
3.某撤信群中四人同时抢3个红包,每人最多抢一个,则其中甲、乙两人都抢到红包的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{1}{2}$ |
4.设全集U={0,-1,-2,-3,-4},集合M={0,-1,-2},那么∁UM为( )
| A. | {0} | B. | {-3,-4} | C. | {-1,-2} | D. | ∅ |