题目内容
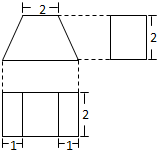
一个几何体的三视图如图所示，则该几何体的表面积是（ ）
A、18+2
| ||
B、24+2
| ||
C、24+4
| ||
D、36+4
|
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：根据三视图判断几何体是直四棱柱，且四棱柱的底面为等腰梯形，棱柱的高为2，底面梯形的上底边长为2，下底边长为4，高为2，利用勾股定理求出腰为
=
，代入棱柱的表面积公式计算．
| 12+22 |
| 5 |
解答：
解：由三视图知几何体是直四棱柱，且四棱柱的底面为等腰梯形，棱柱的高为2，
底面梯形的上底边长为2，下底边长为4，高为2，腰为
=
，
∴几何体的表面积S=（2+4+2
）×2+2×
×2=24+4
．
故选：C．
底面梯形的上底边长为2，下底边长为4，高为2，腰为
| 12+22 |
| 5 |
∴几何体的表面积S=（2+4+2
| 5 |
| 2+4 |
| 2 |
| 5 |
故选：C．
点评：本题考查了由三视图求几何体的表面积，判断三视图的数据所对应的几何量是解答本题的关键．
练习册系列答案
相关题目
若a，b∈R，则以下命题为真的是（ ）
A、若a＞b，则
| ||||
B、若a＞|b|，则
| ||||
| C、若a＞b，则a2＞b2 | ||||
| D、若a＞|b|，则a2＞b2 |
已知函数F（x）=ex满足F（x）=g（x）+h（x），且g（x），h（x）分别是R上的偶函数和奇函数，若?x∈[1，2]使得不等式g（2x）-ah（x）≥0恒成立，则实数a的取值范围是（ ）
A、(-∞，2
| ||
B、(-∞，2
| ||
C、(0，2
| ||
D、(2
|
已知全集U=R，集合A={x|x-1|＜1}，B={x|
≤0}，则A∩（∁UB）=（ ）
| 1-x |
| x |
| A、（0，1） |
| B、[0，1） |
| C、（1，2） |
| D、（0，2） |