题目内容
19.已知抛物线C:y2=4x,直线l:y=-x+b与抛物线交于A,B两点.(Ⅰ)若|AB|=8,求b的值;
(Ⅱ)若以AB为直径的圆与x轴相切,求该圆的方程.
分析 (Ⅰ)由抛物线C:y2=4x,直线l:y=-x+b得y2+4y-4b=0,利用|AB|=8,即可求b的值;
(Ⅱ)若以AB为直径的圆与x轴相切,求出M的坐标,即可求该圆的方程.
解答 解:(Ⅰ)设A(x1,y1),B(x2,y2),由抛物线C:y2=4x,直线l:y=-x+b得y2+4y-4b=0-----(2分)
∴|AB|=$\sqrt{1+\frac{1}{{k}^{2}}}$|y1-y2|=$\sqrt{2}•\sqrt{16+16b}$=$\sqrt{32(b+1)}$=8------------(5分)
解得b=1----------(7分)
(Ⅱ)以AB为直径的圆与x轴相切,设AB中点为M
|AB|=|y1+y2|又y1+y2=-4----------(9分)
∴4=$\sqrt{32(b+1)}$解得b=-$\frac{1}{2}$,则M($\frac{3}{2}$,-2)---------(12分)
∴圆方程为(x-$\frac{3}{2}$)2+(y+2)2=4---------(14分)
点评 本题考查直线与抛物线的位置关系,考查圆的方程,考查韦达定理的运用,属于中档题.

练习册系列答案
相关题目
10.某小学共有学生2000人,其中一至六年级的学生人数分别为400,400,400,300,300,200.为做好小学放学后“快乐30分”活动,现采用分层抽样的方法从中抽取容量为200的样本进行调查,那么应抽取一年级学生的人数为( )
| A. | 120 | B. | 40 | C. | 30 | D. | 20 |
7.如果关于x的不等式x2<ax+b的解集是{x|1<x<3},那么ba等于( )
| A. | -81 | B. | 81 | C. | -64 | D. | 64 |
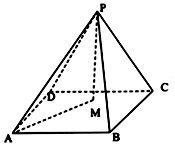 四棱锥P-ABCD中,△PCD为正三角形,底面边长为1的正方形,平面PCD⊥平面ABCD,M为底面内一动点,当$MA=\sqrt{2}PM$时,点M在底面正方形内(包括边界)的轨迹为( )
四棱锥P-ABCD中,△PCD为正三角形,底面边长为1的正方形,平面PCD⊥平面ABCD,M为底面内一动点,当$MA=\sqrt{2}PM$时,点M在底面正方形内(包括边界)的轨迹为( )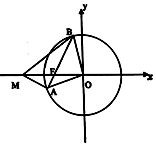 已知圆O:x2+y2=16及圆内一点F(-3,0),过F任作一条弦AB.
已知圆O:x2+y2=16及圆内一点F(-3,0),过F任作一条弦AB. 某飞机失联,经卫星侦查,其最后出现在小岛O附近.现派出四艘搜救船A,B,C,D,为方便联络,船A,B始终在以小岛O为圆心,100海里为半径的圆上,船A,B,C,D构成正方形编队展开搜索,小岛O在正方形编队外(如图).设小岛O到AB的距离为x,∠AOB=α,D船到小岛O的距离为d.
某飞机失联,经卫星侦查,其最后出现在小岛O附近.现派出四艘搜救船A,B,C,D,为方便联络,船A,B始终在以小岛O为圆心,100海里为半径的圆上,船A,B,C,D构成正方形编队展开搜索,小岛O在正方形编队外(如图).设小岛O到AB的距离为x,∠AOB=α,D船到小岛O的距离为d.