题目内容
已知cos(α-
)=-
,sin(
-β)=
,且
<α<2π,
<β<π,求cos
的值.
| β |
| 2 |
| 1 |
| 3 |
| α |
| 2 |
| 1 |
| 4 |
| 3π |
| 2 |
| π |
| 2 |
| α+β |
| 2 |
考点:两角和与差的余弦函数
专题:三角函数的求值
分析:由条件求得π<α-
<
,0<
-β<
.利用同角三角函数的基本关系求得sin(α-
)和cos(
-β)的值,再根据cos
=cos[(α-
)-(
-β)],利用两角差的余弦公式计算求得结果.
| β |
| 2 |
| 3π |
| 2 |
| α |
| 2 |
| π |
| 2 |
| β |
| 2 |
| α |
| 2 |
| α+β |
| 2 |
| β |
| 2 |
| α |
| 2 |
解答:
解:∵
<α<2π,
<β<π,∴π<α-
<
,-
<
-β<
.
∵cos(α-
)=-
,sin(
-β)=
,∴π<α-
<
,0<
-β<
.
∴sin(α-
)=-
=-
,cos(
-β)=
=
.
∴cos
=cos[(α-
)-(
-β)]=cos(α-
)•cos(
-β)+sin(α-
)•sin(
-β)
=-
×
+(-
)×
=-
.
| 3π |
| 2 |
| π |
| 2 |
| β |
| 2 |
| 7π |
| 4 |
| π |
| 4 |
| α |
| 2 |
| π |
| 2 |
∵cos(α-
| β |
| 2 |
| 1 |
| 3 |
| α |
| 2 |
| 1 |
| 4 |
| β |
| 2 |
| 3π |
| 2 |
| α |
| 2 |
| π |
| 2 |
∴sin(α-
| β |
| 2 |
1-cos2(α-
|
2
| ||
| 3 |
| α |
| 2 |
1-sin2(
|
| ||
| 4 |
∴cos
| α+β |
| 2 |
| β |
| 2 |
| α |
| 2 |
| β |
| 2 |
| α |
| 2 |
| β |
| 2 |
| α |
| 2 |
=-
| 1 |
| 3 |
| ||
| 4 |
2
| ||
| 3 |
| 1 |
| 4 |
| ||||
| 12 |
点评:本题主要考查同角三角函数的基本关系、两角和差的三角公式,注意角的范围以及三角函数值的符号,属于中档题.

练习册系列答案
相关题目
满足
=i(i为虚数单位)的复数z=( )
| z+i |
| z |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
一几何体的直观图如图所示,下列给出的四个俯视图中正确的是( )


A、 |
B、 |
C、 |
D、 |
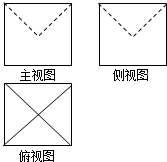 某几何体的三视图如图所示,图中的四边形都是边长为1的正方形,两条虚线互相垂直,则该几何体的体积是( )
某几何体的三视图如图所示,图中的四边形都是边长为1的正方形,两条虚线互相垂直,则该几何体的体积是( )A、
| ||
B、
| ||
C、
| ||
| D、1 |