题目内容
已知两条异面直线a，b的夹角为60°，
，
分别为直线a，b的方向向量，则＜
，
＞= ．
| a |
| b |
| a |
| b |
考点：平面向量数量积的运算
专题：平面向量及应用,空间角
分析：根据异面直线所成角的定义，结合平面向量所成角的定义求出＜
，
＞的角．
| a |
| b |
解答：
解：∵两条异面直线a，b的夹角为60°，
且
，
分别为直线a，b的方向向量，
根据异面直线所成角的定义，
当
，
所成的角是锐角时，
＜
，
＞=60°，
当
，
所成的角是钝角时，
＜
，
＞=120°；
∴＜
，
＞=60°或120°．
故答案为：60°或120°．
且
| a |
| b |
根据异面直线所成角的定义，
当
| a |
| b |
＜
| a |
| b |
当
| a |
| b |
＜
| a |
| b |
∴＜
| a |
| b |
故答案为：60°或120°．
点评：本题考查了直线的方向向量与异面直线的夹角的应用问题，解题时应注意直线夹角与向量夹角的区别与联系，是基础题．
练习册系列答案
相关题目
已知函数f（x）=b-
（x∈[-a，2a-1]）是奇函数，则a+b的值为（ ）
| a |
| 1+2x |
A、
| ||
B、
| ||
| C、2 | ||
| D、-2 |
设函数f（x）=
，则
f（x）dx的值为（ ）
|
| ∫ | 1 -1 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
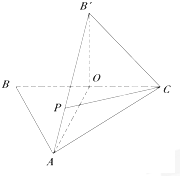如图，△ABC中，O是BC的中点，AB=AC，AO=2OC=2．将△BAO沿AO折起，使B点与图中B'点重合．
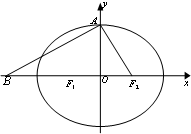设椭圆C：