题目内容
19.已知实数a,b,c满足a2+b=lna,则(a-c)2+(b+c-2)2的最小值为( )| A. | 2$\sqrt{2}$ | B. | 8 | C. | $\sqrt{2}$ | D. | 2 |
分析 根据距离公式可知(a-c)2+(b+c-2)2表示(a,b)到(c,-c+2)的距离的平方,而(a,b)在曲线y=lnx-x2上,(c,-c+2)在直线y=-x+2上,将问题转为求y=lnx-x2的切线与y=-x+2的距离平方.
解答 解:∵a2+b=lna,∴b=lna-a2,
又(c,-c+2)在直线y=-x+2上,
∴(a-c)2+(b+c-2)2的最小值为曲线y=lnx-x2上的点到直线y=-x+2的最小距离的平方.
设直线y=-x+m与曲线y=lnx-x2相切,切点为(x0,y0),
则$\left\{\begin{array}{l}{{y}_{0}=ln{x}_{0}-{{x}_{0}}^{2}}\\{{y}_{0}=-{x}_{0}+m}\\{\frac{1}{{x}_{0}}-2{x}_{0}=-1}\end{array}\right.$,解得x0=1,y0=-1,m=0,
∴直线y=-x与直线y=-x+2的距离为$\frac{2}{\sqrt{2}}$=$\sqrt{2}$,
∴(a-c)2+(b+c-2)2的最小值为2.
故选D.
点评 本题考查了利用导数研究曲线的切线性质、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.命题“?m∈[0,1],x+$\frac{1}{x}≥{2^m}$”的否定形式是( )
| A. | $?m∈[{0,1}],x+\frac{1}{x}<{2^m}$ | B. | $?m∈[{0,1}],x+\frac{1}{x}≥{2^m}$ | C. | $?m∈[{0,1}],x+\frac{1}{x}≤{2^m}$ | D. | $?m∈[{0,1}],x+\frac{1}{x}<{2^m}$ |
4.一个空间几何体的三视图如下,则这个空间几何体的体积是( )
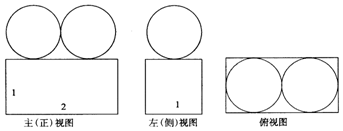

| A. | 2+$\frac{4π}{3}$ | B. | 2+$\frac{π}{3}$ | C. | 1+$\frac{4π}{3}$ | D. | 10+8π |
8.濮阳市黄河滩区某村2010年至2016年人均纯收入(单位:万元)的数据如下表:
(Ⅰ)求y关于x的线性回归方程;
(Ⅱ)利用(Ⅰ)中的回归方程,分析2010年至2016年该村人均纯收入的变化情况,并预测该村2017年人均纯收入.
附:回归直线的斜率和截距的最小乘法估计公式分别为:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{t}$.
| 年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
| 年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(Ⅱ)利用(Ⅰ)中的回归方程,分析2010年至2016年该村人均纯收入的变化情况,并预测该村2017年人均纯收入.
附:回归直线的斜率和截距的最小乘法估计公式分别为:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{t}$.
13.读下面的流程图,若输入的值为-5时,输出的结果是( )


| A. | -10 | B. | -6 | C. | 2 | D. | 8 |