题目内容
4．一个空间几何体的三视图如下，则这个空间几何体的体积是（ ）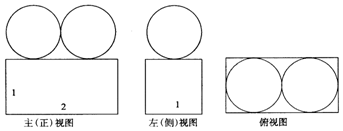
| A． | 2+$\frac{4π}{3}$ | B． | 2+$\frac{π}{3}$ | C． | 1+$\frac{4π}{3}$ | D． | 10+8π |
分析 由三视图得到几何体是两个球与长方体的组合体，根据图中数据计算体积即可．
解答 解：由三视图得到几何体是由半径为0.5的两个球与长宽高分别是2，1，1的长方体组合而成，所以体积为$2×\frac{4}{3}π（\frac{1}{2}）^{3}+2×1×1$=$\frac{π}{3}$+2；
故选：B．
点评 本题考查了几何体的三视图还原几何体；属于基础题．
练习册系列答案
相关题目
15．正项等比数列{an}中，a1+a4+a7=2，a3+a6+a9=18，则{an}的前9项和S9=（ ）
| A． | 14 | B． | 26 | C． | 30 | D． | 29 |
12．已知函数f（x）=（2x-1）ex，a=f（1），b=f（-$\sqrt{2}$），c=f（-ln2），d=f（-$\frac{1}{2}$），则（ ）
| A． | a＞b＞c＞d | B． | b＞a＞c＞d | C． | d＞a＞b＞c | D． | a＞d＞c＞b |
19．已知实数a，b，c满足a2+b=lna，则（a-c）2+（b+c-2）2的最小值为（ ）
| A． | 2$\sqrt{2}$ | B． | 8 | C． | $\sqrt{2}$ | D． | 2 |
9．
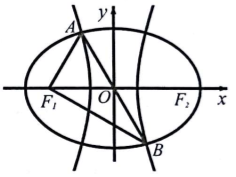如图，F1、F2是椭圆C1与双曲线C2的公共焦点，A、B分别是C1、C2在第二、四象限的公共点，若AF1⊥BF1，且∠AF1O=$\frac{π}{3}$，则C1与C2的离心率之和为（ ）
如图，F1、F2是椭圆C1与双曲线C2的公共焦点，A、B分别是C1、C2在第二、四象限的公共点，若AF1⊥BF1，且∠AF1O=$\frac{π}{3}$，则C1与C2的离心率之和为（ ）| A． | 2$\sqrt{3}$ | B． | 4 | C． | 2$\sqrt{5}$ | D． | 2$\sqrt{6}$ |
