题目内容
椭圆E:
+
=1(a>b>0)与双曲线
-
=1(0<m2<3)有公共的焦点,过椭圆E的右顶点作任意直线l,设直线l交抛物线y2=2x于M、N两点,且OM⊥ON.
(1)求椭圆E的方程;
(2)设P是椭圆E上第一象限内的点,点P关于原点O的对称点为A、关于x轴的对称点为Q,线段PQ与x轴相交于点C,点D为CQ的中点,若直线AD与椭圆E的另一个交点为B,试判断直线PA,PB是否相互垂直?并证明你的结论.
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| m2 |
| y2 |
| 3-m2 |
(1)求椭圆E的方程;
(2)设P是椭圆E上第一象限内的点,点P关于原点O的对称点为A、关于x轴的对称点为Q,线段PQ与x轴相交于点C,点D为CQ的中点,若直线AD与椭圆E的另一个交点为B,试判断直线PA,PB是否相互垂直?并证明你的结论.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)设直线l:ty=x-a,代入y2=2x,并整理,利用韦达定理,结合OM⊥ON,即可求椭圆E的方程;
(2)PA⊥PB,设P(x0,y0),将直线AD的方程y=
(x+x0)-y0代入椭圆的方程,并整理,求出B的坐标,证明kPA•kPB=-1,即可得到结论.
(2)PA⊥PB,设P(x0,y0),将直线AD的方程y=
| y0 |
| 4x0 |
解答:
解:(1)设点M(x1,y1),N(x2,
).
设直线l:ty=x-a,代入y2=2x,并整理得y2-2ty-2a=0,
所以
…(2分)
故有
•
=x1•x2+y1•y2=(ty1+a)(ty2+a)+y1•y2=(t2+1)y1y2+at(y1+y2)+a2
=(t2+1)(-2a)+at2+a2=a2-2a,解得a=2…(5分)
又椭圆与双曲线有公共的焦点,故有c=
,
所以椭圆的方程为
+y2=1.…(7分)
(2)PA⊥PB.
证明:设P(x0,y0),则A(-x0,-y0),D(x0,-
y0)且x02+4
=4
将直线AD的方程y=
(x+x0)-y0代入椭圆的方程,
并整理得(4x02+y02)x2-6x0
+9
-16
=0…(9分)
由题意,可知此方程必有一根-x0,
xB=
+x0,yB=
(
+2x0)-y0=
,
所以kPB=
=
=-
…(12分)
故有kPA•kPB=-1,即PA⊥PB…(13分)
| y | 2 |
设直线l:ty=x-a,代入y2=2x,并整理得y2-2ty-2a=0,
所以
|
故有
| OM |
| ON |
=(t2+1)(-2a)+at2+a2=a2-2a,解得a=2…(5分)
又椭圆与双曲线有公共的焦点,故有c=
| 3 |
所以椭圆的方程为
| x2 |
| 4 |
(2)PA⊥PB.
证明:设P(x0,y0),则A(-x0,-y0),D(x0,-
| 1 |
| 2 |
| y | 2 0 |
将直线AD的方程y=
| y0 |
| 4x0 |
并整理得(4x02+y02)x2-6x0
| y | 2 0 |
| x | 2 0 |
| y | 2 0 |
| x | 2 0 |
由题意,可知此方程必有一根-x0,
xB=
6x0
| ||||
4
|
| y0 |
| 4x0 |
6x0
| ||||
4
|
| ||||
4
|
所以kPB=
| ||||||||||
|
-6
| ||
6x0
|
| x0 |
| y0 |
故有kPA•kPB=-1,即PA⊥PB…(13分)
点评:本题考查直线与抛物线的位置关系,考查椭圆的方程,考查直线与椭圆的位置关系,考查韦达定理的运用,属于中档题.

练习册系列答案
相关题目
下列命题为真命题的是( )
①如果命题“?p”与命题“p∨q”都是真命题,那么命题q一定是真命题;
②“若x2+y2=0,则x,y全为0”的否命题;
③“若x∈A∩B,则x∈A∪B”的逆命题;
④若?p是q的必要条件,则p是?q的充分条件;
⑤到两定点F1(-2,0),F2(2,0)距离之和为定值2的动点轨迹是椭圆.
①如果命题“?p”与命题“p∨q”都是真命题,那么命题q一定是真命题;
②“若x2+y2=0,则x,y全为0”的否命题;
③“若x∈A∩B,则x∈A∪B”的逆命题;
④若?p是q的必要条件,则p是?q的充分条件;
⑤到两定点F1(-2,0),F2(2,0)距离之和为定值2的动点轨迹是椭圆.
| A、①②⑤ | B、①③④ |
| C、②③ | D、①②④ |
执行如图所不的程序框图,则输出的x的值是( )


| A、3 | B、4 | C、6 | D、8 |
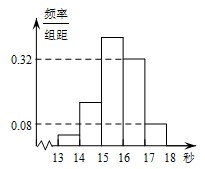 已知某年级1000名学生的百米跑成绩全部介于13秒与18秒之间,为了了解学生的百米跑成绩情况,随机抽取了若干学生的百米跑成绩,并按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为1:4:10,且第二组的频数为8.
已知某年级1000名学生的百米跑成绩全部介于13秒与18秒之间,为了了解学生的百米跑成绩情况,随机抽取了若干学生的百米跑成绩,并按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为1:4:10,且第二组的频数为8.