题目内容
已知函数f(x)=
则关于x的方程f2(x)+bf(x)+c=0有5个不同实数解的充要条件是( )
|
| A、b<-2 且 c>0 |
| B、b>-2 且 c<0 |
| C、b<-2 且 c=0 |
| D、b≥-2 且 c=0 |
考点:充要条件
专题:数形结合
分析:作出f(x)的简图,数形结合可得.
解答:
解:∵方程f2(x)+af(x)+b=0有且只有5个不同实数解,
∴对应于f(x)等于某个常数有4个不同实数解,
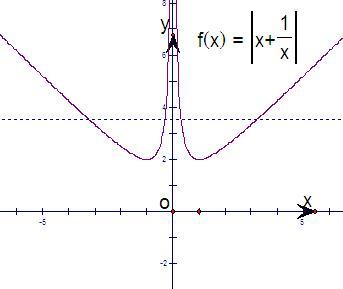
由题意作出f(x)的简图:
由图可知,只有当f(x)=0时,它有-个根.
且f(x)=-b时有四个根,
由图可知-b>2,∴b<-2.
故所求充要条件为:b<-2且c=0,
故选C.
∴对应于f(x)等于某个常数有4个不同实数解,
由题意作出f(x)的简图:
由图可知,只有当f(x)=0时,它有-个根.
且f(x)=-b时有四个根,
由图可知-b>2,∴b<-2.
故所求充要条件为:b<-2且c=0,
故选C.

点评:本题考查方程根的个数问题,数形结合是解决问题的关键,属中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
若0<b<1<a,则下列不等式成立的是( )
| A、ab2<ab<a |
| B、a<ab<ab2 |
| C、ab2<a<ab |
| D、a<ab2<ab |
已知双曲线
-
=1(a>0,b>0)的焦点为F1、F2,过F1作垂直于x轴的直线交双曲线于A、B,若sin∠AF2F1=
,则该双曲线的离心率e=( )
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
| 13 |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |
设二元一次不等式组
所表示的平面区域为M,使函数y=ax(a>0,a≠1)的图象过区域M的a的取值范围是( )
|
| A、[1,3] | ||
B、[2,
| ||
| C、[2,9] | ||
D、[
|
计算复数(
-
i)2的结果为( )
| ||
| 2 |
| ||
| 2 |
| A、i | B、-i | C、1 | D、-1 |
设向量
=(1,0),
=(1,1),则向量
,
的夹角为( )
| OA |
| OB |
| OA |
| OB |
| A、30° | B、45° |
| C、60° | D、90° |