��Ŀ����
5��ij�������з���һ�ֲ�Ʒ�ijɱ�����4Ԫ/����Ϊ�˶Ըò�Ʒ���к������ۣ����ò�Ʒ�������ⶨ�ļ۸�����������õ�����6�����ݣ�| ����x��Ԫ�� | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| ����y������ | 90 | 84 | 83 | 80 | 75 | 68 |
������y����x�����Իع鷽�̣����ûع鷽��Ԥ���ڽ��������У�Ϊʹ�������������ò�Ʒ�ĵ���Ӧ��Ϊ����Ԫ��������L=��������-�ɱ���
�������Իع鷽��$\hat y=\hat bx+\hat a$��ϵ�����㹫ʽ��$\hat b=\frac{{\sum_{i=1}^n{��\;{x_i}-\overline x\;����\;{y_i}-\overline y\;��}}}{{\sum_{i=1}^n{{{��\;{x_i}-\overline x\;��}^2}}}}$��$\hat a=\overline y-\hat b\;\overline x$������$\overline x$��$\overline y$��ʾ������ֵ��
���� ���������⣬�ó�X�Ŀ���ȡֵ�������Ӧ�ĸ���ֵ��д��X�ķֲ�������ѧ����EX��
������$\overline{x}$��$\overline{y}$�����$\stackrel{��}{b}$��$\stackrel{��}{a}$��д��y����x�����Իع鷽�̣��ó�������L��x���Ľ���ʽ�����ö��κ������������L��x�������ֵ���Ӧx��ֵ��
��� �⣺����X�Ŀ���ȡֵΪ0��1��2������90��x+y��100����3�飬
����P��X=0��=$\frac{{C}_{3}^{2}}{{C}_{6}^{2}}$=$\frac{1}{5}$��
P��X=1��=$\frac{{C}_{3}^{1}{•C}_{3}^{1}}{{C}_{6}^{2}}$=$\frac{3}{5}$��
P��X=2��=$\frac{{C}_{3}^{2}}{{C}_{6}^{2}}$=$\frac{1}{5}$��
X�ķֲ���Ϊ
| X | 0 | 1 | 2 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
������Ϊ$\overline{x}$=8.5��$\overline{y}$=80��$\sum_{i=1}^{6}$${{��x}_{i}-\overline{x}��}^{2}$=0.7��$\sum_{i=1}^{6}$��xi-$\overline{x}$����yi-$\overline{y}$��=-14��
����$\stackrel{��}{b}$=$\frac{-14}{0.7}$=-20��$\stackrel{��}{a}$=$\overline{y}$-$\stackrel{��}{b}$$\overline{x}$=250��
y����x�����Իع鷽����$\stackrel{��}{y}$=-20x+250��
������L��x��=x��-20x+250��-4��-20x+250��=-20x2+330x-1000��
��x=-$\frac{330}{2����-20��}$=8.25ʱ��L��x��ȡ�����ֵ361.25��
�ʵ����۶�Ϊ8.25Ԫʱ�������ɻ�����������12�֣�
���� ���⿼������ɢ����������ķֲ����������ļ������⣬Ҳ���������Իع鷽�̵����Լ����κ�������ֵ���⣬���ۺ�����Ŀ��

��ϰ��ϵ�д�
 �Ͻ�ƽ��У����ϵ�д�
�Ͻ�ƽ��У����ϵ�д�
�����Ŀ
13������$\frac{3-i}{i}$=��������
| A�� | 1+3i | B�� | -1-3i | C�� | -1+3i | D�� | 1-3i |
20����֪����P={x|1��x��2}��Q={x|x2-2x��0}����U=R����P��∁UQ=��������
| A�� | [0��2] | B�� | ��0��2] | C�� | ��1��2] | D�� | [1��2] |
10�� ���Ҹ��˵�����һ������й��¡������㡢������Ϸ���ֳ������ȶ���Ԫ�ص����մ��ͻ�����Ϸ���Ŀ������ͨ�˽��������˵�����Ĺ��£���������˶�����Ϊ�䶨�ƵĴ�����Ϸ����Ӯ���˵���������ʽ��������������֮������飬չ���˵�����������е�����Ҹ�̬֮��ij���������ȡ100�������Ŀ�ı����˵��˵��ܶ���Ϊ�������з����о����ɴ˵õ�����Ƶ���ֲ�����
���Ҹ��˵�����һ������й��¡������㡢������Ϸ���ֳ������ȶ���Ԫ�ص����մ��ͻ�����Ϸ���Ŀ������ͨ�˽��������˵�����Ĺ��£���������˶�����Ϊ�䶨�ƵĴ�����Ϸ����Ӯ���˵���������ʽ��������������֮������飬չ���˵�����������е�����Ҹ�̬֮��ij���������ȡ100�������Ŀ�ı����˵��˵��ܶ���Ϊ�������з����о����ɴ˵õ�����Ƶ���ֲ�����
�����������������Щ���ݵ�Ƶ�ʷֲ�ֱ��ͼ��
��������Ƶ����Ϊ���ʣ��Ӳ����Ŀ�ı������������ȡ3λ�������зŻصij����������˵��ܶ���[3000��4000���ڵı�������X�ķֲ��С���ѧ�������뷽�
 ���Ҹ��˵�����һ������й��¡������㡢������Ϸ���ֳ������ȶ���Ԫ�ص����մ��ͻ�����Ϸ���Ŀ������ͨ�˽��������˵�����Ĺ��£���������˶�����Ϊ�䶨�ƵĴ�����Ϸ����Ӯ���˵���������ʽ��������������֮������飬չ���˵�����������е�����Ҹ�̬֮��ij���������ȡ100�������Ŀ�ı����˵��˵��ܶ���Ϊ�������з����о����ɴ˵õ�����Ƶ���ֲ�����
���Ҹ��˵�����һ������й��¡������㡢������Ϸ���ֳ������ȶ���Ԫ�ص����մ��ͻ�����Ϸ���Ŀ������ͨ�˽��������˵�����Ĺ��£���������˶�����Ϊ�䶨�ƵĴ�����Ϸ����Ӯ���˵���������ʽ��������������֮������飬չ���˵�����������е�����Ҹ�̬֮��ij���������ȡ100�������Ŀ�ı����˵��˵��ܶ���Ϊ�������з����о����ɴ˵õ�����Ƶ���ֲ�����| �����˵��˵��ܶԪ�� | [0��1000�� | [1000��2000�� | [2000��3000�� | [3000��4000�� | [4000��5000�� | [5000��6000�� |
| Ƶ�� | 24 | 12 | 32 | 10 | 14 | 8 |
��������Ƶ����Ϊ���ʣ��Ӳ����Ŀ�ı������������ȡ3λ�������зŻصij����������˵��ܶ���[3000��4000���ڵı�������X�ķֲ��С���ѧ�������뷽�
17��ij����һ���и��·ݵ����롢֧�������ͳ����ͼ��ʾ������˵���д�����ǣ�������
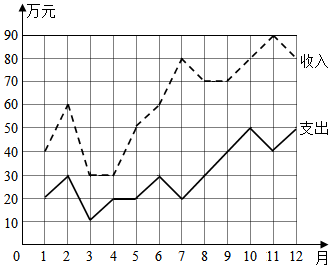
��ע������=����-֧����

��ע������=����-֧����
| A�� | �������ֵ���������ֵ�ı���3��1 | |
| B�� | ������ߵ��·���7�� | |
| C�� | 1��2�·ݵ�����ı仯����4��5�·ݵ�����ı仯����ͬ | |
| D�� | ǰ6���µ�ƽ������Ϊ40��Ԫ |
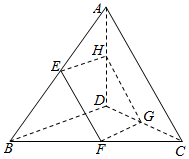 ��ͼ���ڿռ��ı���ABCD�У�E��F��G��H�ֱ���AB��BC��DA���е㣬��AC=BC����֤���ı���EFGH�����Σ�
��ͼ���ڿռ��ı���ABCD�У�E��F��G��H�ֱ���AB��BC��DA���е㣬��AC=BC����֤���ı���EFGH�����Σ�