题目内容
3.若(a2+2b3)n的展开式中有一项为ma4b12,则m=240.分析 利用(a2+2b3)n的展开式中通项公式,结合题意列出方程组求出r、n的值,即可求出m的值.
解答 解:(a2+2b3)n的展开式中通项公式为:
Tr+1=${C}_{n}^{r}$•(x2)n-r•(2b3)r=${C}_{n}^{r}$•2r•a2n-2r•b3r,
根据展开式中有一项为ma4b12,
令$\left\{\begin{array}{l}{2n-2r=4}\\{3r=12}\end{array}\right.$,
解得r=4,n=6;
∴m=${C}_{6}^{4}$•24=240.
故答案为:240.
点评 本题主要考查了利用通项公式求二项式展开式特殊项的应用问题,是基础题.

练习册系列答案
相关题目
11.设α∈($\frac{π}{2}$,π),sinα=$\frac{\sqrt{6}}{3}$,则tan(π+α)等于( )
| A. | -$\sqrt{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
13.将函数$y=sin({2x+\frac{π}{6}})$的图象向左平移$\frac{1}{6}$个周期后,所得图象对应的函数g(x)的一个单调增区间为( )
| A. | [0,π] | B. | $[{-\frac{π}{2},0}]$ | C. | $[{0,\frac{π}{2}}]$ | D. | [-π,0] |
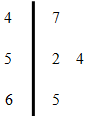 已知某路段最高限速60km/h,电子监控测得连续4辆汽车的速度用用茎叶图表示如图示,若从中任取2辆,则恰好有1辆汽车超速的概率为$\frac{1}{2}$.
已知某路段最高限速60km/h,电子监控测得连续4辆汽车的速度用用茎叶图表示如图示,若从中任取2辆,则恰好有1辆汽车超速的概率为$\frac{1}{2}$.